题目内容
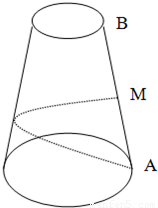
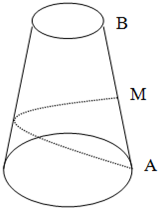如图，圆台上底半径为1，下底半径为4，母线AB=18；从AB的中点M拉一条绳子绕圆台侧面转到点A，则绳子的最短长度为21
21
当绳子最短时，上底圆周上的点到绳子的最短距离为60
| ||
| 7 |
60
| ||
| 7 |
分析：由题意需要画出圆台的侧面展开图，并还原成圆锥展开的扇形，则所求的最短距离是平面图形两点连线，根据条件求出扇形的圆心角以及半径长，在求出最短的距离；取MB′的中点E，连接OE，交圆台上底展开图于F，则EF为所求．
解答：
解：画出圆台的侧面展开图并还原成圆锥展开的扇形，且设扇形的圆心为O．
根据两点之间线段最短，可得所求的最短距离是MB'，
设OA=R，圆心角是α，则
∵圆台上底半径为1，下底半径为4，母线AB=18
∴2π=αR ①，8π=α（18+R） ②，
由①②解得，α=
，R=6，
∴OM=15，OB'=24，
∴由余弦定理可得MB′2=152+242-2×15×24×cos
=441
∴MB′=21．
取MB′的中点E，连接OE，交圆台上底展开图于F，则EF为所求
∴cos∠OMB′=
=
∴OE=
∴EF=
-6
故答案为：21，
-6．
解：画出圆台的侧面展开图并还原成圆锥展开的扇形，且设扇形的圆心为O．根据两点之间线段最短，可得所求的最短距离是MB'，
设OA=R，圆心角是α，则
∵圆台上底半径为1，下底半径为4，母线AB=18
∴2π=αR ①，8π=α（18+R） ②，
由①②解得，α=
| π |
| 3 |
∴OM=15，OB'=24，
∴由余弦定理可得MB′2=152+242-2×15×24×cos
| π |
| 3 |
∴MB′=21．
取MB′的中点E，连接OE，交圆台上底展开图于F，则EF为所求
∴cos∠OMB′=
| 152+10．52-OE2 |
| 2×15×10.5 |
| 152+212-242 |
| 2×15×21 |
∴OE=
60
| ||
| 7 |
∴EF=
60
| ||
| 7 |
故答案为：21，
60
| ||
| 7 |
点评：本题考查在几何体表面的最短距离，一般方法是把几何体的侧面展开后，根据题意作出最短距离即两点连线，结合条件求出，考查了转化思想．
练习册系列答案
出彩同步大试卷系列答案
相关题目
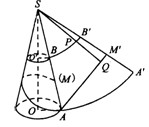
如图，圆台上底半径为1，下底半径为4，母线AB=18；从AB的中点M拉一条绳子绕圆台侧面转到点A，则绳子的最短长度为________当绳子最短时，上底圆周上的点到绳子的最短距离为________．