题目内容
已知长度相等的三个非零向量 、
、 ,满足
,满足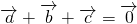 ,求每两个向量之间的夹角.
,求每两个向量之间的夹角.
解:设 的夹角为θ
的夹角为θ
∵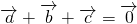
∴
∴
即
∵三向量的长度相等
cosθ=
∴θ=120°
即 的夹角为120°
的夹角为120°
同理每两个向量之间的夹角都是120°
分析:将其中一个向量 移到等式的一边,两边平方,利用向量的模等于向量的平方,向量的数量积公式及已知条件求出两个向量
移到等式的一边,两边平方,利用向量的模等于向量的平方,向量的数量积公式及已知条件求出两个向量 的夹角.同理求出
的夹角.同理求出 的夹角.
的夹角.
点评:本题考查向量的数量积公式及利用向量的数量积求向量的夹角.
 的夹角为θ
的夹角为θ∵
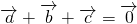
∴

∴

即

∵三向量的长度相等
cosθ=

∴θ=120°
即
 的夹角为120°
的夹角为120°同理每两个向量之间的夹角都是120°
分析:将其中一个向量
 移到等式的一边,两边平方,利用向量的模等于向量的平方,向量的数量积公式及已知条件求出两个向量
移到等式的一边,两边平方,利用向量的模等于向量的平方,向量的数量积公式及已知条件求出两个向量 的夹角.同理求出
的夹角.同理求出 的夹角.
的夹角.点评:本题考查向量的数量积公式及利用向量的数量积求向量的夹角.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 、
、 ,满足
,满足 ,求每两个向量之间的夹角.
,求每两个向量之间的夹角.