题目内容
已知长度相等的三个非零向量| a |
| b |
| c |
| a |
| b |
| c |
| 0 |
分析:将其中一个向量
移到等式的一边,两边平方,利用向量的模等于向量的平方,向量的数量积公式及已知条件求出两个向量
,
的夹角.同理求出
,
及
,
的夹角.
| c |
| a |
| b |
| a |
| c; |
| b |
| c |
解答:解:设
,
的夹角为θ
∵
+
+
=
∴
+
= -
∴
2+
2+2
•
=
2
即|
|2+ |
|2 +2|
||
|cosθ=|
|2
∵三向量的长度相等
cosθ=-
∴θ=120°
即
,
的夹角为120°
同理每两个向量之间的夹角都是120°
| a |
| b |
∵
| a |
| b |
| c |
| 0 |
∴
| a |
| b |
| c |
∴
| a |
| b |
| a |
| b |
| c |
即|
| a |
| b |
| a |
| b |
| c |
∵三向量的长度相等
cosθ=-
| 1 |
| 2 |
∴θ=120°
即
| a |
| b |
同理每两个向量之间的夹角都是120°
点评:本题考查向量的数量积公式及利用向量的数量积求向量的夹角.

练习册系列答案
相关题目
 、
、 ,满足
,满足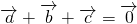 ,求每两个向量之间的夹角.
,求每两个向量之间的夹角. 、
、 ,满足
,满足 ,求每两个向量之间的夹角.
,求每两个向量之间的夹角.