题目内容
如图,平面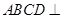 平面
平面 ,四边形
,四边形 是正方形,四边形
是正方形,四边形 是矩形,且
是矩形,且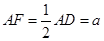 ,
,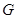 是
是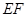 的中点,则
的中点,则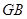 与平面
与平面 所成角的正弦值为( )
所成角的正弦值为( )
A.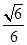 | B.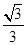 | C.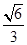 | D. |
C
解析试题分析:由已知可知图中直线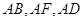 两两垂直,因此我们以此为空间的直角坐标轴建立空间直角坐标系,利用向量法求出
两两垂直,因此我们以此为空间的直角坐标轴建立空间直角坐标系,利用向量法求出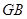 与平面
与平面 所成角的正弦值.
所成角的正弦值.
考点:用向量法求直线与平面所成的角.

练习册系列答案
相关题目
已知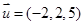 ,
,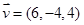 ,
,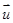 ,
,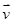 分别是平面
分别是平面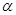 ,
,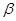 的法向量,则平面
的法向量,则平面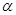 ,
,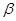 的位置关系式( )
的位置关系式( )
| A.平行 | B.垂直 |
| C.所成的二面角为锐角 | D.所成的二面角为钝角 |
设点 关于原点的对称点为
关于原点的对称点为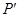 ,则
,则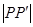 等于( )
等于( )
A.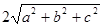 | B.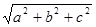 | C.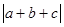 | D.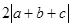 |
.如图,在四面体OABC中,G是底面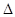 ABC的重心,则
ABC的重心,则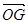 等于
等于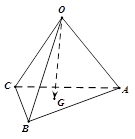
A.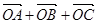 | B.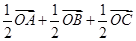 |
C.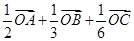 | D.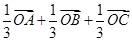 |
已知点A(1,1,1),点B(-3,-3,-3),则线段AB的长为
A.4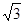 | B.2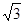 | C.4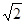 | D.3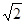 |
若向量
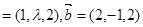 ,且
,且 与
与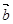 的夹角余弦值为
的夹角余弦值为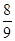 ,则
,则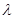 等于( )
等于( )
A.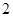 | B.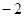 | C.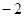 或 或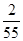 | D.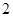 或 或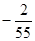 |
△ABC的顶点分别为A(1,-1,2),B(5,-6,2),C(1,3,-1)则AC边上的高BD等于( )
| A.2 |
B.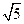 |
| C.5 |
| D.6 |
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F且EF=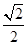 ,则下列结论中错误的是 ( ).
,则下列结论中错误的是 ( ).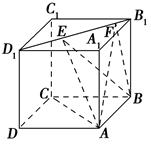
| A.AC⊥BE |
| B.EF∥平面ABCD |
| C.三棱锥A-BEF的体积为定值 |
| D.异面直线AE,BF所成的角为定值 |