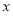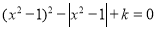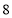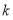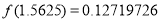题目内容
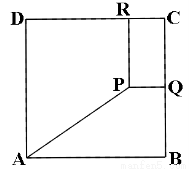
在边长为10的正方形 内有一动点
内有一动点 ,
, ,作
,作 于
于 ,
, 于
于 ,求矩形
,求矩形 面积的最小值和最大值,并指出取最大值时
面积的最小值和最大值,并指出取最大值时 的具体位置.
的具体位置.
最小值为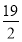 ;最大值为
;最大值为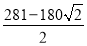 ,此时
,此时 点处在
点处在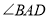 的角平分线上,且满足
的角平分线上,且满足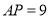 .
.
【解析】
试题分析:本题是函数模型的建立与应用问题,解题的关键是引入适当的变量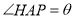 ,建立面积
,建立面积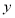 与
与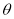 的三角函数模型
的三角函数模型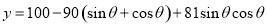 ,然后根据同角三角函数的基本关系式,令
,然后根据同角三角函数的基本关系式,令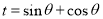 ,再将模型转化为关于
,再将模型转化为关于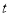 的二次函数
的二次函数 模型,转化时要特别注意变量取值范围的变化,最后利用二次函数的性质求取函数的最值,并确定取得最大值点
模型,转化时要特别注意变量取值范围的变化,最后利用二次函数的性质求取函数的最值,并确定取得最大值点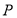 的位置.
的位置.
试题解析:连结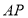 ,延长
,延长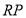 交
交 于
于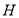 ,设
,设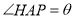
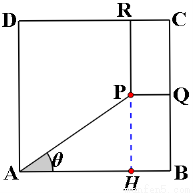
则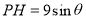 ,
,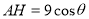
设矩形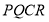 的面积为
的面积为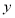 ,则
,则
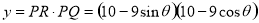
 4分
4分
设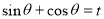 ,则
,则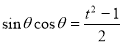
又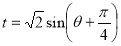 ,
,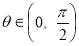
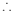
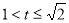
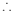
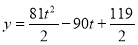
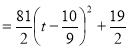 (
(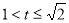 ) 8分
) 8分
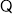
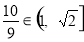
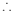 当
当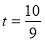 时,
时,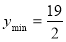 10分
10分
当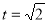 时,
时,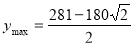
此时, ,又
,又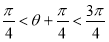
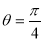 13分.
13分.
考点:1.函数的应用;2.二次函数的最值;3.三角函数的性质.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目