题目内容
已知函数 (
( 为常数,且
为常数,且 ),对于定义域内的任意两个实数
),对于定义域内的任意两个实数 、
、 ,恒有
,恒有 成立,则正整数
成立,则正整数 可以取的值有
可以取的值有
| A.4个 | B.5个 | C.6 个 | D.7个 |
B
解析试题分析:定义域为 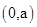 ,又
,又 ,所以
,所以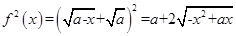 ,易知
,易知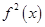 的最大值为
的最大值为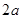 ,最小值为a,所以
,最小值为a,所以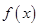 的最大值为
的最大值为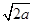 ,最小值为
,最小值为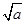 。要满足对于定义域内的任意两个实数
。要满足对于定义域内的任意两个实数 、
、 ,恒有
,恒有 成立,只需
成立,只需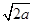 -
-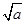 <1,解得
<1,解得 ,所以正整数
,所以正整数 可以取的值有1,2,3,4,5,共有5个。
可以取的值有1,2,3,4,5,共有5个。
考点:函数的最值;函数的单调性。
点评:直接研究函数 的单调性和最值,不易研究,我们可以采取平方的方法进行转化后在研究,这是做此题的关键。
的单调性和最值,不易研究,我们可以采取平方的方法进行转化后在研究,这是做此题的关键。

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
函数 的零点所在的区间为 ( )
的零点所在的区间为 ( )
A.(1, ) ) | B.( ,2) ,2) | C.(2,e) | D.(e,+∞) |
设偶函数 在
在 上是增函数,则
上是增函数,则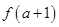 与
与 的
的
大小关系是( )
A. | B. |
C. | D.不能确定 |
下列函数中是偶函数且在 上单调递增的是 ( )
上单调递增的是 ( )
A. | B. | C. | D. |
若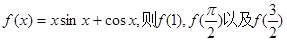 的大小关系是( )
的大小关系是( )
A.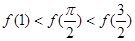 | B. |
C. | D.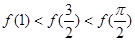 |
函数 的定义域是
的定义域是
A.( ) ) | B.( | C. | D. ) ) |
关于狄利克雷函数 的叙述错误的是 ( )
的叙述错误的是 ( )
A. 的值域是 的值域是 | B. 是偶函数 是偶函数 |
C. 是奇函数 是奇函数 | D. 的定义域是 的定义域是 |
 的图像大致是
的图像大致是
 在区间
在区间 上是增函数,实数
上是增函数,实数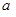 组成集合
组成集合 ;设关于
;设关于 的方程
的方程 的两个非零实根
的两个非零实根 实数
实数 使得不等式
使得不等式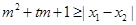 使得对任意
使得对任意 及
及 恒成立,则
恒成立,则


