题目内容
(本小题13分)
设等比数列![]() 的前项和为
的前项和为![]() ,首项
,首项![]() ,公比
,公比![]() .
.
(I)证明:![]() ;
;
(II)若数列![]() 满足
满足![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(III)记![]() ,
,![]() ,数列
,数列![]() 的前项和为
的前项和为![]() ,求证:当
,求证:当![]() 时,
时,![]() .
.
(1)见解析(2)![]() (3)见解析
(3)见解析
解析:
(I)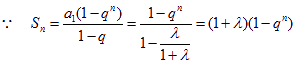 2分
2分
又![]()
![]()
![]() 4分
4分
(II)![]() ,
,![]() 得
得![]() 6分
6分
即![]() 是以
是以![]() 为首项,
为首项,![]() 为公差的等差数列.
为公差的等差数列.
![]() ,即
,即![]() . 8分
. 8分
(III)当![]() 时,
时,![]() ,
,![]() 9分
9分
![]() ①
①
![]() ②
②
①-②得
![]()
![]() 12分
12分
又易知数列![]() 是单调递增的,故当
是单调递增的,故当![]() 时,
时,![]()
即当![]() 时,
时,![]() 13分
13分

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
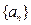 的前项和为
的前项和为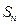 ,首项
,首项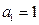 ,公比
,公比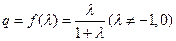 .
.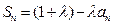 ;
;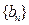 满足
满足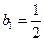 ,
,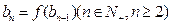 ,求数列
,求数列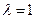 ,
,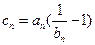 ,数列
,数列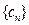 的前项和为
的前项和为 ,求证:当
,求证:当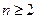 时,
时,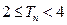 .
.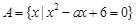 ,
,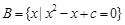 ,且A∩B={2},
,且A∩B={2},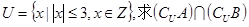

 的单调性;
的单调性; ,记过点
,记过点 的直线的斜率为
的直线的斜率为 ,问:是否存在
,问:是否存在 ,使得
,使得 若存在,求出
若存在,求出