题目内容
已知数列{an}中,a1=1,a1+2a2+3a3+…+nan=
(Ⅰ)求数列{an}的通项an;
(2)求数列{n2an}的前n项和Tn;
(3)若存在n∈N*,使得an≥(n+1)λ成立,求实数λ的取值范围.
解:(1)因为a1+2a2+3a3+…+nan=
所以a1+2a2+3a3+…+(n-1)an-1=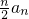 (n≥2)
(n≥2)
两式相减得nan=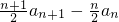
所以 =3(n≥2)
=3(n≥2)
因此数列{nan}从第二项起,是以2为首项,以3为公比的等比数列
所以nan=2•3n-2(n≥2)
故an=
(2)由(1)可知当n≥2n2an=2n•3n-2
当n≥2时,Tn=1+4•30+6•31+…+2n•3n-2,
∴3Tn=3+4•31+…+2(n-1)•3n-2+2n•3n-1,
两式相减得 (n≥2)
(n≥2)
又∵T1=a1=1也满足上式,
所以Tn=
(3)an≥(n+1)λ等价于λ≤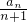 ,
,
由(1)可知当n≥2时,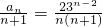
设f(n)= ,
,
则f(n+1)-f(n)= <0,
<0,
∴ ,又
,又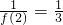 及
及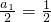 ,
,
∴所求实数λ的取值范围为λ≤
分析:(1)因为a1+2a2+3a3+…+nan= ,所以a1+2a2+3a3+…+(n-1)an-1=
,所以a1+2a2+3a3+…+(n-1)an-1=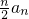 (n≥2.所以
(n≥2.所以 =3(n≥2).由此能够求出an.
=3(n≥2).由此能够求出an.
(2)由(1)可知当n≥2n2an=2n•3n-2.当n≥2时,Tn=1+4•30+6•31+…+2n•3n-2,由错位相减法得到 (n≥2),又因为T1=a1=1也满足上式,所以Tn=
(n≥2),又因为T1=a1=1也满足上式,所以Tn= .
.
(3)an≥(n+1)λ等价于λ≤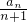 ,当n≥2时,
,当n≥2时,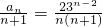 ,设f(n)=
,设f(n)= ,则f(n+1)-f(n)=
,则f(n+1)-f(n)= <0,由此能求出实数λ的取值范围.
<0,由此能求出实数λ的取值范围.
点评:本题首先考查等差数列、等比数列的基本量、通项,结合含两个变量的不等式的处理问题,对数学思维的要求比较高,要注意错位相减求和法和转化与化归思想的合理运用,本题有一定的探索性.综合性强,难度大,易出错.

所以a1+2a2+3a3+…+(n-1)an-1=
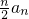 (n≥2)
(n≥2)两式相减得nan=
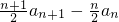
所以
 =3(n≥2)
=3(n≥2)因此数列{nan}从第二项起,是以2为首项,以3为公比的等比数列
所以nan=2•3n-2(n≥2)
故an=

(2)由(1)可知当n≥2n2an=2n•3n-2
当n≥2时,Tn=1+4•30+6•31+…+2n•3n-2,
∴3Tn=3+4•31+…+2(n-1)•3n-2+2n•3n-1,
两式相减得
 (n≥2)
(n≥2)又∵T1=a1=1也满足上式,
所以Tn=

(3)an≥(n+1)λ等价于λ≤
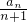 ,
,由(1)可知当n≥2时,
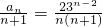
设f(n)=
 ,
,则f(n+1)-f(n)=
 <0,
<0,∴
 ,又
,又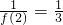 及
及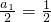 ,
,∴所求实数λ的取值范围为λ≤

分析:(1)因为a1+2a2+3a3+…+nan=
 ,所以a1+2a2+3a3+…+(n-1)an-1=
,所以a1+2a2+3a3+…+(n-1)an-1=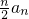 (n≥2.所以
(n≥2.所以 =3(n≥2).由此能够求出an.
=3(n≥2).由此能够求出an.(2)由(1)可知当n≥2n2an=2n•3n-2.当n≥2时,Tn=1+4•30+6•31+…+2n•3n-2,由错位相减法得到
 (n≥2),又因为T1=a1=1也满足上式,所以Tn=
(n≥2),又因为T1=a1=1也满足上式,所以Tn= .
.(3)an≥(n+1)λ等价于λ≤
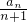 ,当n≥2时,
,当n≥2时,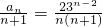 ,设f(n)=
,设f(n)= ,则f(n+1)-f(n)=
,则f(n+1)-f(n)= <0,由此能求出实数λ的取值范围.
<0,由此能求出实数λ的取值范围.点评:本题首先考查等差数列、等比数列的基本量、通项,结合含两个变量的不等式的处理问题,对数学思维的要求比较高,要注意错位相减求和法和转化与化归思想的合理运用,本题有一定的探索性.综合性强,难度大,易出错.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|