题目内容
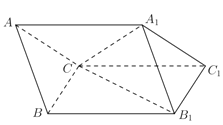
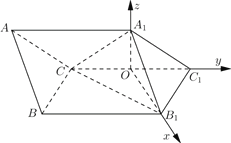
【题目】如图,斜三棱柱![]() 中,侧面
中,侧面![]() 与侧面
与侧面![]() 都是菱形,
都是菱形, ![]() ,
, ![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)根据题设条件,证明![]() ,得到
,得到![]() 平面
平面![]() ,即可证明
,即可证明![]() ;(Ⅱ)以
;(Ⅱ)以![]() 为原点,分别以
为原点,分别以![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,求得平面
,求得平面![]() 的一个法向量
的一个法向量![]() ,即可利用向量所成的角,得出直线与平面所成的角.
,即可利用向量所成的角,得出直线与平面所成的角.
试题解析:(Ⅰ)连接![]() ,因为侧面
,因为侧面![]() 与侧面
与侧面![]() 都是菱形,
都是菱形,
![]() ,所以
,所以![]() 都是等边三角形.
都是等边三角形.
取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,
,
又![]() 平面
平面![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,
,
所以![]() .
.
(Ⅱ)在![]() 中,
中, ![]() ,若
,若![]() ,则有
,则有![]() ,
,
所以![]() ,
,
由(Ⅰ)有![]() 平面
平面![]() ,
,
以![]() 为原点,分别以
为原点,分别以![]() 所在直线为
所在直线为![]() 轴,
轴,
建立空间直角坐标系![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则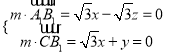
整理,得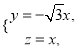
令![]() ,得
,得![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则
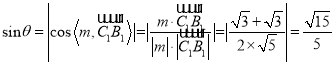 .
.
所以直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】已知某校5个学生的数学和物理成绩如表
学生的编号i | 1 | 2 | 3 | 4 | 5 |
数学xi | 80 | 75 | 70 | 65 | 60 |
物理yi | 70 | 66 | 68 | 64 | 62 |
(Ⅰ)假设在对这5名学生成绩进行统计时,把这5名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有2名学生的物理成绩是自己的实际分数的概率是多少?
(Ⅱ)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用x表示数学成绩,用y表示物理成绩,求y与x的回归方程;
参考公式: ![]() =
= 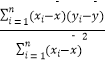 ,
, ![]() .
.