题目内容
已知命题p:函数 在(0,1)内恰有一个零点;命题q:函数
在(0,1)内恰有一个零点;命题q:函数 在
在 上是减函数,若p且
上是减函数,若p且 为真命题,则实数a的取值范围是( )
为真命题,则实数a的取值范围是( )
A. | B.a≤2 | C.1<a≤2 | D.a≤l或a>2 |
C
解析试题分析:由题知,命题 :
: ,得
,得 ,命题
,命题 :
: ,则
,则 ,若
,若 且
且 为真命题,则有
为真命题,则有 ,故实数
,故实数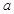 的取值范围是
的取值范围是 .
.
考点:1、函数的零点;2、幂函数的图象和性质;3、复合命题的真假.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
命题“若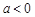 ,则一元二次方程
,则一元二次方程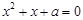 有实根”的原命题与其逆命题、否命题、逆否命题中真命题的个数是( )
有实根”的原命题与其逆命题、否命题、逆否命题中真命题的个数是( )
| A.0 | B.2 | C.4 | D.不确定 |
设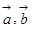 为向量。则
为向量。则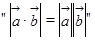 是
是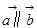 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也必要条件 |
“|x-1|<2成立”是“x(x-3)<0成立”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知命题p:“?x∈[1,2],x2-a≥0”,命题q:“?x∈R”,x2+2ax+2-a=0,若命题“p∧q”是真命题,则实数a的取值范围是( )
| A.a≤-2或a=1 | B.a≤-2或1≤a≤2 |
| C.a≥1 | D.-2≤a≤1 |
设 ,则“
,则“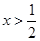 ”是“
”是“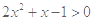 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题:①至少有一个x使x2+2x+1=0成立;②对任意的x都有x2+2x+1=0成立;
③对任意的x都有x2+2x+1=0不成立;④存在x使x2+2x+1=0成立.
其中是全称命题的有( )
| A.1个 | B.2个 | C.3个 | D.0个 |
“ ”是“
”是“ ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充分必要条件 | D.既非充分又非必要条件 |
命题:“若 ,则
,则 ”的逆否命题是( )
”的逆否命题是( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 ,则 ,则 | D.若 ,或 ,或 ,则 ,则 |