题目内容
正四棱柱ABCD-A1B1C1D1,E、F、G、H分分别为AA1、BB1、CC1、DD1的中点,FD与底面成30°夹角,若底面边长为2,则四棱柱的高等于
- A.
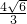
- B.2
- C.

- D.

A
分析:由正四棱柱ABCD-A1B1C1D1,结构特征,得∠FDB为FD与底面成的角,从而有∠FDB=30°,解得BD=2 ,再解棱长的一半,FD=BD•tan300=
,再解棱长的一半,FD=BD•tan300= 从而求得四棱柱的高.
从而求得四棱柱的高.
解答:由正四棱柱ABCD-A1B1C1D1,
得∠FDB为FD与底面成的角
∴∠FDB=300
BD=2
∴FD=BD•tan300=
∴四棱柱的高等于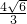
点评:本题主要考查空间几何体的结构特征和线面角的求法.要先找或作出线面角,再用三角形的知识求解.
分析:由正四棱柱ABCD-A1B1C1D1,结构特征,得∠FDB为FD与底面成的角,从而有∠FDB=30°,解得BD=2
 ,再解棱长的一半,FD=BD•tan300=
,再解棱长的一半,FD=BD•tan300= 从而求得四棱柱的高.
从而求得四棱柱的高.解答:由正四棱柱ABCD-A1B1C1D1,
得∠FDB为FD与底面成的角
∴∠FDB=300
BD=2

∴FD=BD•tan300=

∴四棱柱的高等于
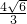
点评:本题主要考查空间几何体的结构特征和线面角的求法.要先找或作出线面角,再用三角形的知识求解.

练习册系列答案
相关题目
顶点在同一球面上的正四棱柱ABCD-A′B′C′D′中,AB=1,AA′=
,则A、C两点间的球面距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
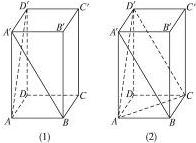 如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是
如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是