题目内容
6.已知函数g(x)=(a+1)x-2+1(a>0)的图象恒过定点A,且点A又在函数$f(x)={log_{\sqrt{3}}}$(x+a)的图象上.则实数a=1.分析 令x-2=0得x=2并求出g(2),可得定点A的坐标,由题意代入f(x)的解析式,由对数的运算性质化简后求出a的值.
解答 解:令x-2=0得x=2,则g(2)=(a+1)0+1=2,
所以函数g(x)的图象恒过定点A(2,2),
代入$f(x)=lo{g}_{\sqrt{3}}$(x+a)得,2+a=${(\sqrt{3})}^{2}$,
解得a=1,
故答案为:1.
点评 本题考查指数函数的图象过定点问题,属于基础题.

练习册系列答案
相关题目
11.执行如图所示的程序,则输入的i的值为( )


| A. | -1 | B. | 0 | C. | -1或2 | D. | 2 |
15.经过A(0,-1),B(2,3)的直线的斜率等于( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
16.若xlog32≥-1,则函数f(x)=4x-2x+1-3的最小值为( )
| A. | -4 | B. | -3 | C. | $-\frac{32}{9}$ | D. | 0 |
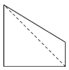
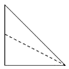
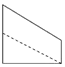
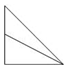
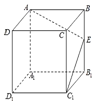 如图,点E为正方体ABCD-A1B1C1D1的棱BB1的中点,用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )
如图,点E为正方体ABCD-A1B1C1D1的棱BB1的中点,用过点A,E,C1的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )