题目内容
已知向量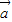 =(cosα,sinα),
=(cosα,sinα),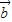 =(cosβ,sinβ)且
=(cosβ,sinβ)且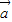 与
与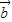 满足关系式:|k
满足关系式:|k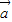 +
+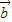 |=
|=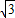 |
|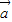 -k
-k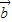 |(其中k>0).
|(其中k>0).(1)用k表示
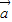 •
•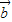 ;
;(2)证明:
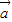 与
与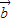 不垂直;
不垂直;(3)当
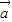 与
与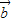 的夹角为60°时,求k的值.
的夹角为60°时,求k的值.
【答案】分析:(1)由题意可得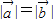 =1,把已知条件平方可得结果;
=1,把已知条件平方可得结果;
(2)由(1)的结果结合基本不等式可证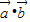
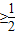 ,故不垂直;
,故不垂直;
(3)由数量积的定义结合前面所求可建立关于k的方程,解之即可.
解答:解:(1)∵|k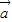 +
+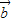 |=
|=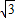 |
|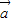 -k
-k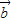 |,
|,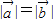 =1,
=1,
∴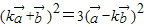 ,化简可得:
,化简可得:
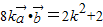 ,故
,故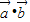 =
=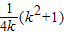 (k>0);
(k>0);
(2)由(1)可得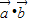 =
=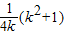 (k>0),
(k>0),
由基本不等式可得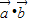 =
=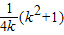 =
= (k+
(k+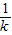 )
)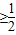 ,
,
当且仅当k=1时取等号,故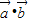 ≠0,
≠0,
故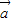 与
与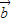 不垂直;
不垂直;
(3)当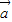 与
与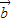 的夹角为60°时,
的夹角为60°时,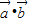 =
=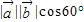 =
= ,
,
又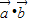 =
=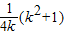 (k>0),
(k>0),
∴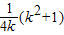 =
= ,解得k=1
,解得k=1
点评:本题为向量的综合应用,涉及向量的模长夹角和基本不等式,属中档题.
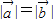 =1,把已知条件平方可得结果;
=1,把已知条件平方可得结果;(2)由(1)的结果结合基本不等式可证
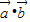
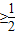 ,故不垂直;
,故不垂直;(3)由数量积的定义结合前面所求可建立关于k的方程,解之即可.
解答:解:(1)∵|k
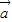 +
+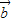 |=
|=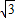 |
|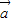 -k
-k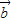 |,
|,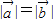 =1,
=1,∴
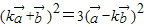 ,化简可得:
,化简可得: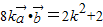 ,故
,故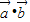 =
=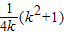 (k>0);
(k>0);(2)由(1)可得
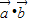 =
=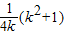 (k>0),
(k>0),由基本不等式可得
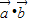 =
=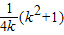 =
= (k+
(k+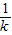 )
)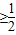 ,
,当且仅当k=1时取等号,故
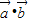 ≠0,
≠0,故
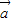 与
与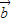 不垂直;
不垂直;(3)当
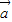 与
与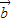 的夹角为60°时,
的夹角为60°时,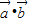 =
=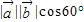 =
= ,
,又
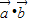 =
=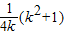 (k>0),
(k>0),∴
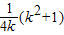 =
= ,解得k=1
,解得k=1点评:本题为向量的综合应用,涉及向量的模长夹角和基本不等式,属中档题.

练习册系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |