题目内容
如图,M(-2,0)和N(2,0)是平面上的两点,动点P满足:||PM|-|PN||=2.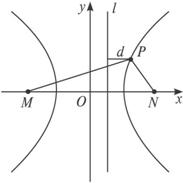
(1)求点P的轨迹方程;
(2)设d为点P到直线l:x=![]() 的距离,若|PM|=2|PN|2,求
的距离,若|PM|=2|PN|2,求![]() 的值.
的值.
(1)解:由双曲线的定义,点P的轨迹是以M、N为焦点,实轴长2a=2的双曲线,因此半焦距c=2,实半轴a=1,从而虚半轴b=![]() .
.
所以双曲线的方程为x2![]() =1.
=1.
(2)解法一:由(1)及图(1),易知|PN|≥1,因|PM|=2|PN|2, ①

(1)?
知|PM|>|PN|,故P为双曲线右支上的点,所以|PM|=|PN|+2. ②
将②代入①,得2|PN|2-|PN|-2=0,解得|PN|=![]() ,舍去
,舍去![]() ,所以|PN|=
,所以|PN|=![]() .
.
因为双曲线的离心率e=![]() =2,直线l:x=
=2,直线l:x=![]() 是双曲线的右准线,故
是双曲线的右准线,故![]() =e=2,所以d=
=e=2,所以d=![]() |PN|,
|PN|,
因此![]() =
=![]() =
=![]() =4|PN|=1+
=4|PN|=1+![]() .
.
解法二:设P(x,y).因|PN|≥1知|PM|=2|PN|2≥2|PN|>|PN|,故P在双曲线右支上,所以x≥1.由双曲线方程有y2=3x2-3,
因此|PM|=![]() =
=![]() =
=![]() =2x+1.
=2x+1.
|PN|=![]() =
=![]() =
=![]() .
.
从而由|PM|=2|PN|2得2x+1=2(4x2-4x+1),即8x2-10x+1=0.
所以x=![]() (舍去x=
(舍去x=![]() ).
).
有|PM|=2x+1=![]() ,d=x-
,d=x-![]() =
=![]() .
.
故![]() =
=![]() ·
·![]() =1+
=1+![]() .
.

练习册系列答案
相关题目