题目内容
PA垂直于△ABC所在的平面,若AB=AC=13,BC=10,PA=12,则P到BC的距离为
- A.12
- B.10
- C.13
- D.
D
分析:过点A作AD⊥BC,垂足为D,连接P,D.由AB=AC,知BD= BC.由BC=10,知BD=5.在Rt△ABD中,由AB=13,知AD=12.由PA⊥平面ABC,知BC⊥平面PAD,由此能求出点P到BC的距离.
BC.由BC=10,知BD=5.在Rt△ABD中,由AB=13,知AD=12.由PA⊥平面ABC,知BC⊥平面PAD,由此能求出点P到BC的距离.
解答:过点A作AD⊥BC,垂足为D,连接P,D
∵AB=AC∴BD= BC,
BC,
∵BC=10,∴BD=5
在Rt△ABD中:AB=13,∴AD=12
∵PA⊥平面ABC
∴PA⊥AD,PA⊥BC
∴BC⊥平面PAD,
∴BC⊥PD,∴PD为点P到BC的距离
在Rt△PAD中:PA=12,∴PD=12√2
∴点P到BC的距离为12 .
.
点评:本题考查点、线、面间的距离的计算,解题时要认真审题,注意立体几何知识的合理运用.
分析:过点A作AD⊥BC,垂足为D,连接P,D.由AB=AC,知BD=
 BC.由BC=10,知BD=5.在Rt△ABD中,由AB=13,知AD=12.由PA⊥平面ABC,知BC⊥平面PAD,由此能求出点P到BC的距离.
BC.由BC=10,知BD=5.在Rt△ABD中,由AB=13,知AD=12.由PA⊥平面ABC,知BC⊥平面PAD,由此能求出点P到BC的距离.解答:过点A作AD⊥BC,垂足为D,连接P,D
∵AB=AC∴BD=
 BC,
BC,∵BC=10,∴BD=5
在Rt△ABD中:AB=13,∴AD=12
∵PA⊥平面ABC
∴PA⊥AD,PA⊥BC
∴BC⊥平面PAD,
∴BC⊥PD,∴PD为点P到BC的距离
在Rt△PAD中:PA=12,∴PD=12√2
∴点P到BC的距离为12
 .
.点评:本题考查点、线、面间的距离的计算,解题时要认真审题,注意立体几何知识的合理运用.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 7、如图所示,AB是圆O的直径,C是异于A,B两点的圆周上的任意一点,PA垂直于圆O所在的平面,则△PAB,△PAC,△ABC,△PBC中,直角三角形的个数是( )
7、如图所示,AB是圆O的直径,C是异于A,B两点的圆周上的任意一点,PA垂直于圆O所在的平面,则△PAB,△PAC,△ABC,△PBC中,直角三角形的个数是( ) 14、如图所示,AB是圆O的直径,C是异于A,B两点的圆周上的任意一点,PA垂直于圆O所在的平面,则△PAB,△PAC,△ABC,△PBC中,直角三角形的个数是
14、如图所示,AB是圆O的直径,C是异于A,B两点的圆周上的任意一点,PA垂直于圆O所在的平面,则△PAB,△PAC,△ABC,△PBC中,直角三角形的个数是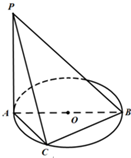 如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.
如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.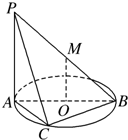 如图所示,直线PA垂直于⊙O所在的平面,△ABC内接于⊙O,且AB为⊙O的直径,点M为线段PB的中点.现有结论:①BC⊥PC;②OM∥平面APC;③点B到平面PAC的距离等于线段BC的长.其中正确的是( )
如图所示,直线PA垂直于⊙O所在的平面,△ABC内接于⊙O,且AB为⊙O的直径,点M为线段PB的中点.现有结论:①BC⊥PC;②OM∥平面APC;③点B到平面PAC的距离等于线段BC的长.其中正确的是( )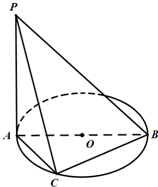 如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.
如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.