题目内容
等差数列{an}的首项为a1,公差为d,Sn点为前n项和,则数列{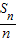 }是( )
}是( )A.首项为a1,公差为d的等差数列
B.首项为a1,公差为
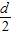 的等差数列
的等差数列C.首项为a1,公比为d的等比数列
D.首项为a1,公比为
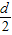 的等比数列
的等比数列
【答案】分析:依题意,可知等差数列{an}的前n项和Sn=na1+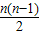 d,从而可求得
d,从而可求得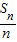 的关系式,从而可得答案.
的关系式,从而可得答案.
解答:解:∵等差数列{an}的首项为a1,公差为d,前n项和为Sn,
则Sn=na1+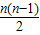 d,
d,
∴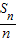 =a1+
=a1+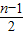 •d
•d
=a1+(n-1)•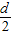 .
.
∴数列{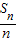 }是以a1为首项,
}是以a1为首项,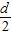 为公差的等差数列,
为公差的等差数列,
故选B.
点评:本题考查等差关系的确定,突出考查等差数列的求和公式与等差数列的定义,属于中档题.
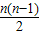 d,从而可求得
d,从而可求得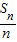 的关系式,从而可得答案.
的关系式,从而可得答案.解答:解:∵等差数列{an}的首项为a1,公差为d,前n项和为Sn,
则Sn=na1+
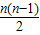 d,
d,∴
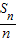 =a1+
=a1+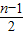 •d
•d=a1+(n-1)•
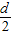 .
.∴数列{
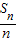 }是以a1为首项,
}是以a1为首项,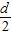 为公差的等差数列,
为公差的等差数列,故选B.
点评:本题考查等差关系的确定,突出考查等差数列的求和公式与等差数列的定义,属于中档题.

练习册系列答案
相关题目