题目内容
已知a1=1数列{an}的前n项和Sn满足nSn+1-(n+3)Sn=0
(1)求an
( 2 ) .
.
解:(1)∵nSn+1-(n+3)Sn=0,即nan+1=3Sn①
∴(n-1)an=3Sn-1(n≥2)②
①-②得nan+1=(n+2)an(n≥2)
∴an= ×
× ×
× ×…×
×…× ×
× ×
× ×
×
= (n≥2),
(n≥2),
a1=1也适合上式,
∴an= (n∈N*).
(n∈N*).
(2)bn= =
=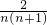 =2(
=2( -
- ),
),
∴Tn=2(1- +
+ -
- +…+
+…+ -
- )
)
= .
.
分析:(1)由nSn+1-(n+3)Sn=0①下推一项可得(n-1)an=3Sn-1(n≥2)②,两式作差可求得nan+1=(n+2)an(n≥2),利用累乘法可求得an;
(2)由(1)可求得an= (n∈N*),利用裂项法可得bn=
(n∈N*),利用裂项法可得bn= =2(
=2( -
- ),继而可求得Tn.
),继而可求得Tn.
点评:本题考查数列的求和,突出累乘法求通项与裂项法求和的应用,由nSn+1-(n+3)Sn=0下推一项可得(n-1)an=3Sn-1(n≥2)后作差是解决问题的关键,考查观察与分析问题、解决问题的能力,属于中档题.
∴(n-1)an=3Sn-1(n≥2)②
①-②得nan+1=(n+2)an(n≥2)
∴an=
 ×
× ×
× ×…×
×…× ×
× ×
× ×
×
=
 (n≥2),
(n≥2),a1=1也适合上式,
∴an=
 (n∈N*).
(n∈N*).(2)bn=
 =
=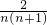 =2(
=2( -
- ),
),∴Tn=2(1-
 +
+ -
- +…+
+…+ -
- )
)=
 .
.分析:(1)由nSn+1-(n+3)Sn=0①下推一项可得(n-1)an=3Sn-1(n≥2)②,两式作差可求得nan+1=(n+2)an(n≥2),利用累乘法可求得an;
(2)由(1)可求得an=
 (n∈N*),利用裂项法可得bn=
(n∈N*),利用裂项法可得bn= =2(
=2( -
- ),继而可求得Tn.
),继而可求得Tn.点评:本题考查数列的求和,突出累乘法求通项与裂项法求和的应用,由nSn+1-(n+3)Sn=0下推一项可得(n-1)an=3Sn-1(n≥2)后作差是解决问题的关键,考查观察与分析问题、解决问题的能力,属于中档题.

练习册系列答案
相关题目