题目内容
在区间 上随机取一实数
上随机取一实数 ,则该实数
,则该实数 满足不等式
满足不等式 的概率为( )
的概率为( )
A. | B. | C. | D. |
B
解析试题分析:解不等式1≤log2x≤2,可得2≤x≤4,以长度为测度,即可求在区间[0,9]上随机取一实数x,该实数x满足不等式1≤log2x≤2的概率解:本题属于几何概型,解不等式1≤log2x≤2,可得2≤x≤4,∴在区间[0,9]上随机取一实数x,该实数x满足不等式1≤log2x≤2的概率为 故答案为B
故答案为B
考点:几何概型
点评:本题考查几何概型,解题的关键是解不等式,确定其测度

练习册系列答案
相关题目
下图是正态分布N(0,1)的正态曲线图,下面3个式子中,等于图中阴影部分面积的个数为( )。注:Φ P
P

① ②
②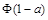 ③
③
| A.0 | B.1 | C.2 | D.3 |
已知正三棱锥 的底面边长为
的底面边长为 ,高为
,高为 ,在正三棱锥内任取一点
,在正三棱锥内任取一点 ,使得
,使得 的概率为( )
的概率为( )
A. | B. | C. | D. |
某射击运动员射击所得环数ξ的分布列如下所示,则P(ξ=8)=( )
| ξ | 7 | 8 | 9 | 10 |
| P | 0.21 | m | 0.29 | 0.22 |
下列叙述正确的是
A.任何事件的概率总是在 之间 之间 |
| B.频率是客观存在的,与试验次数无关 |
| C.随着试验次数的增加,频率一般会越来越接近概率 |
| D.概率是随机的,在试验前不能确定 |
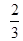 ,则阴影区域的面积为( )
,则阴影区域的面积为( ) 



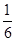
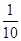

 ( )
( )


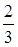
 )等于( )
)等于( )


