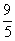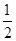题目内容
已知正三棱锥 的底面边长为
的底面边长为 ,高为
,高为 ,在正三棱锥内任取一点
,在正三棱锥内任取一点 ,使得
,使得 的概率为( )
的概率为( )
A. | B. | C. | D. |
A
解析试题分析:本题利用几何概型解决.根据题中条件:“VP-ABC< 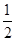 VS-ABC”得点P所在的区域为棱锥的中截面以下,结合大棱锥与小棱锥的体积比即可求得结果.解:由题意知,当点P在三棱锥的中截面以下时,满足: VP-ABC<
VS-ABC”得点P所在的区域为棱锥的中截面以下,结合大棱锥与小棱锥的体积比即可求得结果.解:由题意知,当点P在三棱锥的中截面以下时,满足: VP-ABC<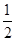 VS-ABC,故使得VP-ABC<
VS-ABC,故使得VP-ABC<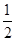 VS-ABC的概率为:(大棱锥的体积-小棱锥的体积):大棱锥的体积=1-
VS-ABC的概率为:(大棱锥的体积-小棱锥的体积):大棱锥的体积=1- .故选A
.故选A
考点:几何概型
点评:本题主要考查了几何概型,以及空间想象能力,属于基础题.简单地说,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型,解本题的关键是理解体积比是相似比的平方

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
某学生解选择题出错的概率为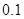 ,该生解三道选择题至少有一道出错的概率是( )
,该生解三道选择题至少有一道出错的概率是( )
A.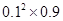 | B.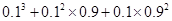 |
C.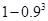 | D.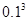 |
掷两颗骰子,所得点数之和为 ,那么
,那么 =4表示的随机试验结果是( )
=4表示的随机试验结果是( )
| A.一颗是3点,一颗是1点 | B.两颗都是2点 |
| C.两颗都是4点 | D.一颗是3点,一颗是1点或两颗都是2点 |
在区间 上随机取一实数
上随机取一实数 ,则该实数
,则该实数 满足不等式
满足不等式 的概率为( )
的概率为( )
A. | B. | C. | D. |
已知某一随机变量ξ的概率分布列如下,且E(ξ)=6.3,则a的值为( )
| ξ | 4 | a | 9 |
| P | 0.5 | 0.1 | b |
已知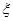 ~
~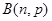 ,且
,且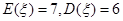 ,则
,则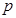 等于( )
等于( )
A.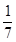 | B.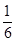 | C.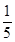 | D.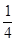 |
 ,
, =
=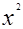 +
+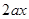 -
- +
+

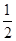

 ,则甲回家途中遇红灯次数的期望为( )
,则甲回家途中遇红灯次数的期望为( )