题目内容
已知△ABC,点D与A在BC的同侧,且∠A=∠D,求证:A、B、C、D四点共圆.
图
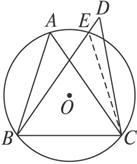
证明:如图
(1)假设D在⊙O外部,⊙O与BD交于E点,连结CE.
∵![]() =
=![]() ,∴∠A=∠BEC.
,∴∠A=∠BEC.
又∠D=∠A,∴∠BEC=∠D.
这与三角形的外角大于任何一个不相邻的内角相矛盾.
故点D不在⊙O外部.
(2)假设D在⊙O内部,延长BD交⊙O于E,连结CE,如图
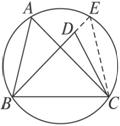
图
则有∠A=∠E.
又∠A=∠BDC,
∴∠BDC=∠E.
同样产生矛盾.
∴点D不能在圆内.
综上所述,点D只能在圆周上,即A、B、C、D四点共圆.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知△ABC的三个顶点A、B、C及平面内一点P,若
+
+
=
,则点P与△ABC的位置关系是( )
| PA |
| PB |
| PC |
| BC |
| A、P在AB边上 |
| B、P在AC边上或其延长线上 |
| C、P在△ABC的内部 |
| D、P在△ABC的外部 |
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.