题目内容
已知函数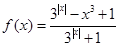
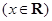 的最大值为
的最大值为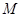 ,最小值为
,最小值为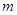 ,
,
则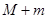 的值为 .
的值为 .
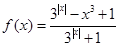
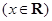 的最大值为
的最大值为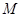 ,最小值为
,最小值为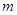 ,
,则
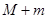 的值为 .
的值为 .
试题分析:因为
 ,而
,而 利用奇偶性定义可知,g(-x)=-g(x)是奇函数,那么可知f(x)就是奇函数向上平移一个单位得到的,那么奇函数中最大值和最小值的和为零,向上平移一个单位后,那么利用对称性可知,最大值和最小值关于(0,1)对称,故M+m=2.答案为2.
利用奇偶性定义可知,g(-x)=-g(x)是奇函数,那么可知f(x)就是奇函数向上平移一个单位得到的,那么奇函数中最大值和最小值的和为零,向上平移一个单位后,那么利用对称性可知,最大值和最小值关于(0,1)对称,故M+m=2.答案为2.点评:解决该试题的关键是能很好的利用奇偶性的对称性质,得到所求解函数关于(0,1)
中心对称,那么结合对称性得到结论。

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 kg)与上市时间t(单位:天)的数据如下表:
kg)与上市时间t(单位:天)的数据如下表: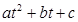 , Q= a
, Q= a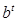 , Q=a
, Q=a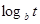 .
.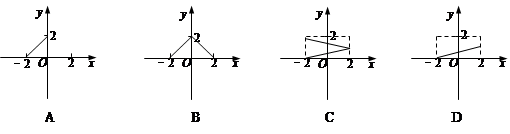
 满足:
满足: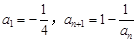 ,则
,则 =( )
=( )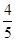
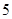


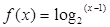 。
。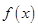 的零点;
的零点; )=1,③对任意x,y
)=1,③对任意x,y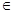 ( 0,+∞),
( 0,+∞),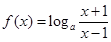 (
(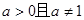 ).
).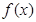 的奇偶性,并证明;
的奇偶性,并证明;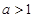 ,用单调性定义证明函数
,用单调性定义证明函数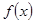 在区间
在区间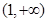 上单调递减;
上单调递减;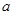 ,使得
,使得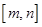 时,值域为
时,值域为 ,若存在,求出实数
,若存在,求出实数 ,若实数
,若实数 是方程
是方程 的解,且
的解,且 ,则
,则 的值是( )
的值是( )