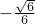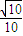题目内容
 将等腰直角三角形ABC沿斜边BC上的高AD折起,使折后△ABC恰为等边三角形,M为BD的中点,则直线AB与CM所成角的余弦值为( )
将等腰直角三角形ABC沿斜边BC上的高AD折起,使折后△ABC恰为等边三角形,M为BD的中点,则直线AB与CM所成角的余弦值为( )分析:由折叠后△ABC恰为等边三角形,推断出BD⊥DC,从而DA,DB,DC互相垂直,可以以D为坐标原点,建立空间直角坐标系,运用空间向量的知识方法求解.
解答: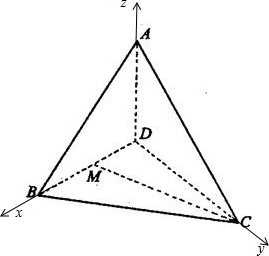 解:设AD=1,则BD=CD=1,AB=AC=
解:设AD=1,则BD=CD=1,AB=AC=
,因为折后△ABC为等边三角形,∴BC=
,在△BDC中,BD2+DC2=BC2,∴BD⊥DC.
以D为坐标原点,建立空间直角坐标系,如图
则A(0,0,1),B(1,0,0),C(0,1,0),M(
,0,0)
∴
=(1,0,-1),
=(
,-1,0)
cos<
,
>=
=
=
.
∴则直线AB与CM所成角的余弦值为
.
故选C.
 解:设AD=1,则BD=CD=1,AB=AC=
解:设AD=1,则BD=CD=1,AB=AC=| 2 |
| 2 |
以D为坐标原点,建立空间直角坐标系,如图
则A(0,0,1),B(1,0,0),C(0,1,0),M(
| 1 |
| 2 |
∴
| AB |
| CM |
| 1 |
| 2 |
cos<
| AB |
| CM |
| ||||
|
|
| ||||||
|
| ||
| 10 |
∴则直线AB与CM所成角的余弦值为
| ||
| 10 |
故选C.
点评:本题考查异面直线夹角的计算,利用了空间向量的方法.利用向量的方法,思路相对固定,能降低思维难度,正确的应用计算公式是关键,易错点是有时不能够准确写出相关点和向量的坐标.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
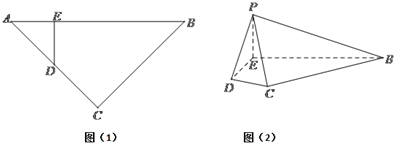
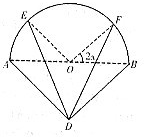 如图,实线部分是某公园设计的游客观光路线平面图,曲线部分是以AB为直径的半圆,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米,
如图,实线部分是某公园设计的游客观光路线平面图,曲线部分是以AB为直径的半圆,点O为圆心,△ABD是以AB为斜边的等腰直角三角形,其中AB=2千米, 将等腰直角三角形ABC沿斜边BC上的高AD折起,使折后△ABC恰为等边三角形,M为BD的中点,则直线AB与CM所成角的余弦值为
将等腰直角三角形ABC沿斜边BC上的高AD折起,使折后△ABC恰为等边三角形,M为BD的中点,则直线AB与CM所成角的余弦值为