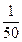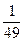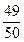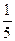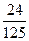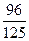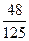题目内容
将一颗骰子投掷两次,第一次出现的点数记为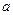 ,第二次出现的点数记为
,第二次出现的点数记为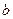 ,
,
设两条直线l1:ax+by=2,l2:x+2y=2平行的概率为P1,相交的概率为P2,试问点(P1,P2)与直线l2:x+2y=2的位置关系是
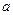 ,第二次出现的点数记为
,第二次出现的点数记为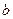 ,
,设两条直线l1:ax+by=2,l2:x+2y=2平行的概率为P1,相交的概率为P2,试问点(P1,P2)与直线l2:x+2y=2的位置关系是
| A.P在直线l2的右下方 | B.P在l2直线的左下方 |
| C.P在直线l2的右上方 | D.P在直线l2上 |
B
易知当且仅当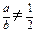 时两条直线只有一个交点,而满足
时两条直线只有一个交点,而满足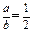 的情况有三种:
的情况有三种: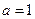 ,
,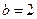 (此时两直线重合),
(此时两直线重合),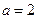 ,
,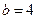 (此时两直线平行),
(此时两直线平行),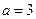 ,
,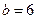 (此时两直线平行),而投掷两次的所有情况有6×6=36种,所以两条直线相交的概率P2=1-
(此时两直线平行),而投掷两次的所有情况有6×6=36种,所以两条直线相交的概率P2=1-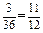 ;两条直线平行的概率为P1=
;两条直线平行的概率为P1= ,所求点P是(
,所求点P是(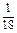 ,
,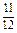 ),易判断P(
),易判断P(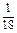 ,
,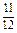 )在直线
)在直线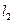 的左下方.
的左下方.
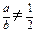 时两条直线只有一个交点,而满足
时两条直线只有一个交点,而满足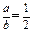 的情况有三种:
的情况有三种: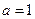 ,
,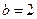 (此时两直线重合),
(此时两直线重合),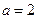 ,
,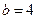 (此时两直线平行),
(此时两直线平行),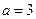 ,
,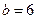 (此时两直线平行),而投掷两次的所有情况有6×6=36种,所以两条直线相交的概率P2=1-
(此时两直线平行),而投掷两次的所有情况有6×6=36种,所以两条直线相交的概率P2=1-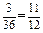 ;两条直线平行的概率为P1=
;两条直线平行的概率为P1= ,所求点P是(
,所求点P是(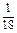 ,
,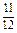 ),易判断P(
),易判断P(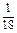 ,
,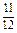 )在直线
)在直线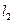 的左下方.
的左下方.
练习册系列答案
相关题目
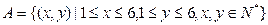
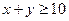 的概率
的概率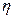 为随机变量,
为随机变量,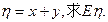 w.&
w.&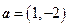 ,
,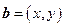 .
. 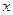 ,
, 分别表示将一枚质地均匀的正方体骰子(六个面
分别表示将一枚质地均匀的正方体骰子(六个面 的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足
的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次、第二次出现的点数,求满足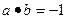 的
的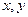
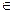
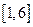 ,求满足
,求满足 的概率.
的概率.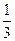 ,得到黑球或黄球的概率是
,得到黑球或黄球的概率是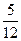 ,得到黄球或绿球的概率也是
,得到黄球或绿球的概率也是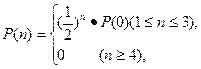 那么在某一时刻,这个公用电话亭里一个人也没有的概率是___________.
那么在某一时刻,这个公用电话亭里一个人也没有的概率是___________.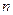 的球的重量为
的球的重量为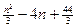 (克). 这些球以等可能性(不受重量, 号码的影响)从袋里取出.
(克). 这些球以等可能性(不受重量, 号码的影响)从袋里取出.