题目内容
过点C(12,16)作圆x2+y2=100的两条切线,切点为A、B,则点C到直线AB的距离为( )
| A、5 | ||
B、
| ||
| C、10 | ||
| D、15 |
分析:根据题意,以C为圆心、CA长为半径作圆C,可得B点在圆C上,因此直线AB是圆O与圆C的公共弦所在直线.利用圆的切线性质与勾股定理算出圆C的半径,得到圆C的方程进而求出直线AB的方程,最后利用点到直线的距离公式加以计算,可得点C到直线AB的距离.
解答:解: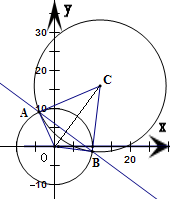 圆x2+y2=100的圆心为O(0,0),半径r=10.
圆x2+y2=100的圆心为O(0,0),半径r=10.
连结OA、OB、OC,可得|OC|=
=20,
∵AC切圆O与点A,
∴OA⊥AC,
|AC|=
=10
,
因此,以C为圆心、CA半径的圆方程为(x-12)2+(y-16)2=300,
∵CA、CB为经过点C的圆O的两条切线,
∴|AC|=|BC|,可得点B也在圆C上,因此AB是圆O与圆C的公共弦,
将圆O与圆C的方程相减,得3x+4y-25=0,
可得点C到直线AB的距离d=
=15.
故选:D
 圆x2+y2=100的圆心为O(0,0),半径r=10.
圆x2+y2=100的圆心为O(0,0),半径r=10.连结OA、OB、OC,可得|OC|=
| 122+162 |
∵AC切圆O与点A,
∴OA⊥AC,
|AC|=
| |OC|2-|OA|2 |
| 3 |
因此,以C为圆心、CA半径的圆方程为(x-12)2+(y-16)2=300,
∵CA、CB为经过点C的圆O的两条切线,
∴|AC|=|BC|,可得点B也在圆C上,因此AB是圆O与圆C的公共弦,
将圆O与圆C的方程相减,得3x+4y-25=0,
可得点C到直线AB的距离d=
| |3×12+4×16-25| | ||
|
故选:D
点评:本题给出圆O的经过点C的两条切线,求切点弦所在直线与点C的距离.着重考查了圆的切线的性质、点到直线的距离公式和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
