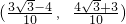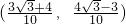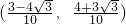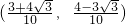题目内容
圆心在第一象限，且半径为1的圆与抛物线y2=2x的准线和双曲线
-
=1的渐近线都相切，则圆心的坐标是
| x2 |
| 16 |
| y2 |
| 9 |
（
，
） 或（
，
）
| 1 |
| 2 |
| 13 |
| 8 |
| 1 |
| 2 |
| 7 |
| 8 |
（
，
） 或（
，
）
．| 1 |
| 2 |
| 13 |
| 8 |
| 1 |
| 2 |
| 7 |
| 8 |
分析：根据双曲线的标准方程，求出渐近线方程，结合条件设出圆心坐标，再利用点到直线的距离公式求得参数，从而得到所求．
解答：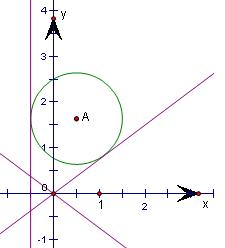
解：由双曲线方程可得a=4，b=3，c=5，
渐近线方程y=
和y=-
，即3x-4y=0和3x+4y=0．
抛物线y2=2x的准线为：x=-
，
根据圆心在第一象限，且半径为1的圆与抛物线y2=2x的准线相切，
设圆心A的坐标为（
，m），（m＞0）．
①当圆与双曲线
-
=1的渐近线3x-4y=0相切时，
圆心A到直线3x-4y=0的距离即为圆的半径1，
即
=1，⇒m=
；
②当圆与双曲线
-
=1的渐近线3x+4y=0相切时，
圆心A到直线3x+4y=0的距离即为圆的半径1，
即
=1，⇒m=
；
则圆心的坐标是：（
，
） 或（
，
）．
故答案为：（
，
） 或（
，
）．
解：由双曲线方程可得a=4，b=3，c=5，渐近线方程y=
| 3x |
| 4 |
| 3x |
| 4 |
抛物线y2=2x的准线为：x=-
| 1 |
| 2 |
根据圆心在第一象限，且半径为1的圆与抛物线y2=2x的准线相切，
设圆心A的坐标为（
| 1 |
| 2 |
①当圆与双曲线
| x2 |
| 16 |
| y2 |
| 9 |
圆心A到直线3x-4y=0的距离即为圆的半径1，
即
|3×
| ||
|
| 13 |
| 8 |
②当圆与双曲线
| x2 |
| 16 |
| y2 |
| 9 |
圆心A到直线3x+4y=0的距离即为圆的半径1，
即
|3×
| ||
|
| 7 |
| 8 |
则圆心的坐标是：（
| 1 |
| 2 |
| 13 |
| 8 |
| 1 |
| 2 |
| 7 |
| 8 |
故答案为：（
| 1 |
| 2 |
| 13 |
| 8 |
| 1 |
| 2 |
| 7 |
| 8 |
点评：本题考查双曲线的标准方程，以及双曲线的简单性质的应用，点到直线的距离公式，圆的标准方程，求半径是解题的关键．
练习册系列答案
相关题目
已知F1，F2分别是双曲线
的左、右焦点，以坐标原点O为圆心，以双曲线的半焦距c为半径的圆与双曲线在第一象限的交点为A，与y轴正半轴的交点为B，点A在y轴上的射影为H，且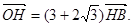
的值．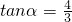
．将角α终边逆时针旋转
大小的角后与单位圆交于点Q，则点Q的坐标为
