Question

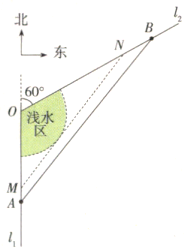
【题目】某港湾的平面示意图如图所示，、、分别是海岸线、上的三个集镇，位于的正南方向处，位于的北偏东方向处.随着经济的发展，为缓解集镇的交通压力，拟在海岸线、上分别修建码头、，开辟水上航线，勘测时发现：以为圆心，为半径的扇形区域为浅水区，不适宜船只航行.

（1）能否求出集镇、间的直线距离？

（2）根据勘测要求，要使、之间的直线航线最短，直线与圆应满足什么关系？

（3）应怎样确定码头、的位置，才能使得、之间的直线航线最短？

Answer 1

【答案】（1）；（2）直线与圆应该相切；（3）码头、与集镇的距离均为时，、之间的直线航线最短.

【解析】

（1）在中，利用余弦定理可求出的长度；

（2）要使、之间的直线航线最短，又使得航线不能经过浅水区，进而可得知直线与圆的位置关系；

（3）设直线与圆相切于点，连接，设，，，根据的面积得到等式，然后利用余弦定理结合基本不等式求出的最小值，利用等号成立的条件求出、，进而可得出结论.

（1）在中，，，，

根据余弦定理得，所以，故集镇、间的直线距离为；

（2）要使、之间的直线航线最短，又使得航线不能经过浅水区，则直线与圆应该相切；

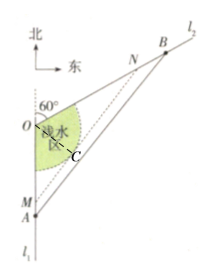
（3）设直线与圆相切于点，连接，则.

设，，，

在中，由，

得，即，

由余弦定理，得，

所以，解得，

当且仅当时，取得最小值，

所以码头、与集镇的距离均为时，、之间的直线航线最短，最短距离为.