题目内容
【题目】已知函数![]() 的图象在
的图象在![]() 处的切线过点
处的切线过点![]() ,
, ![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极值点;
的极值点;
(2)设![]() 是函数
是函数![]() 的两个极值点,若
的两个极值点,若![]() ,证明:
,证明: ![]() .(提示
.(提示![]() )
)
【答案】(1)![]() 或2;(2)见解析
或2;(2)见解析
【解析】试题分析:(1)求导![]() ,则
,则![]() .又
.又![]() ,曲线
,曲线![]() 在
在![]() 处的切线过点
处的切线过点![]() 利用斜率相等
利用斜率相等![]() ,可得
,可得![]() .,又
.,又![]() ,可得
,可得![]() ,则
,则![]() ,可得函数
,可得函数![]() 的极值点
的极值点
(2)由题![]() 是方程
是方程![]() 的两个根,则
的两个根,则![]() ,
, ![]() ,由
,由![]() ,可得
,可得![]() ,
, ![]() ,∴
,∴![]() 是函数
是函数![]() 的极大值,
的极大值, ![]() 是函数
是函数![]() 的极小值,∴要证
的极小值,∴要证![]() ,只需
,只需![]() ,计算整理可得
,计算整理可得![]()
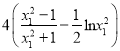 ,令
,令![]() ,则
,则![]() ,设
,设![]() ,利用导数讨论函数
,利用导数讨论函数![]()
的性质即可得证
试题解析;∵![]() ,∴
,∴![]() .又
.又![]() ,曲线
,曲线![]() 在
在![]() 处的切线过点
处的切线过点![]() .∴
.∴![]() ,得
,得![]() .
.
(1)∵![]() ,∴
,∴![]() ,令
,令![]() ,得
,得![]() ,
,
解得![]() 或2,∴
或2,∴![]() 的极值点为
的极值点为![]() 或2.
或2.
(2)∵![]() 是方程
是方程![]() 的两个根,∴
的两个根,∴![]() ,
, ![]() ,∵
,∵![]() ,∴
,∴![]() ,
, ![]() ,∴
,∴![]() 是函数
是函数![]() 的极大值,
的极大值, ![]() 是函数
是函数![]() 的极小值,∴要证
的极小值,∴要证![]() ,只需
,只需![]() ,
, ![]()
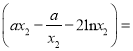
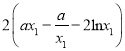
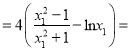
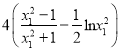 ,令
,令![]() ,则
,则![]() ,设
,设![]()
![]() ,则
,则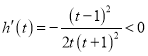 ,函数
,函数![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,∴
,∴![]()
![]()

练习册系列答案
相关题目