Question

设函数y=sinx（0≤x≤π）的图象为曲线C，动点A（x，y）在曲线C上，过A且平行于x轴的直线交曲线C于另一点B（A，B可以重合），设线段AB的长关于x的函数为y=f（x），其图象可以为（　　）

A．

B．

C．

D．

Answer 1

分析：由已知可得线段AB的长y=f（x）=

-2x+π，当0≤x≤ π 2 时 2x-π，当 π 2 ＜x≤π时

，据此可选出其图象．

解答：解：作出函数y=sinx（0≤x≤π）的图象，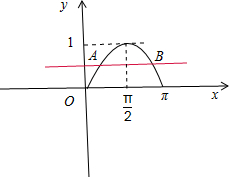
由图象可知：当x=0或π时，y=π；当x=

π

2

时，f(

π

2

)=0；
又当0＜x＜

π

2

时，线段AB的长随着x的增大而减小，且f（x）=π-x-x=-2x+π；
又当

π

2

＜x≤π时，线段AB的长随着x的增大而增大，且f（x）=x-（π-x）=2x-π．
综上可知线段AB的长y=f（x）=

-2x+π，当0≤x≤ π 2 时 2x-π，当 π 2 ＜x≤π时

，据此可知其图象为C．
故选C．

点评：由已知条件正确求出函数y=f（x）的表达式是解题的关键．