题目内容
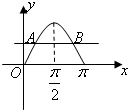 设函数y=sinx(0≤x≤π)的图象为曲线C,动点A(x,y)在曲线C上,过A且平行于x轴的直线交曲线C于点B(A、B可以重合),设线段AB的长为f(x),则函数f(x)在[0,
设函数y=sinx(0≤x≤π)的图象为曲线C,动点A(x,y)在曲线C上,过A且平行于x轴的直线交曲线C于点B(A、B可以重合),设线段AB的长为f(x),则函数f(x)在[0,| π |
| 2 |
递减
递减
,在[| π |
| 2 |
递增
递增
.分析:线段AB的长为f(x),即为AB的横坐标差的绝对值,根据正弦函数的单调性,即可得到结论.
解答:解:线段AB的长为f(x),即为AB的横坐标差的绝对值,根据函数y=sinx(0≤x≤π)在[0,
]上单调增,在[
,π]上单调减,可得函数f(x)在[0,
]上单调递减,在[
,π]上单调递增
故答案为:递减,递增
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
故答案为:递减,递增
点评:本题考查函数的单调性,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
相关题目
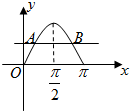 设函数y=sinx(0≤x≤π)的图象为曲线C,动点A(x,y)在曲线C上,过A且平行于x轴的直线交曲线C于点B(A、B可以重合),设线段AB的长为f(x),则函数f(x)单调递增区间
设函数y=sinx(0≤x≤π)的图象为曲线C,动点A(x,y)在曲线C上,过A且平行于x轴的直线交曲线C于点B(A、B可以重合),设线段AB的长为f(x),则函数f(x)单调递增区间