题目内容

棱长为2的正方体ABCD-A1B1C1D1中，
BC1
•
B1D1
=（　　）
A、2
2
B、4
C、-2
2
D、-4
分析：利用
BC1
与 
B1D1
的夹角等于
BC1
与BD的夹角，等于60°，向量的模等于棱长的
2
倍，代入两个向量的数量积的定义计算．
解答：解：棱长为2的正方体ABCD-A1B1C1D1中，
BC1
与 
B1D1
的夹角等于
BC1
与BD的夹角，等于60°．
∴
BC1
•
B1D1
=2
2
×2
2
cos60°=4，
故选B．
点评：本题考查两个向量的数量积的定义，关键是求出两个向量的夹角．
练习册系列答案
相关题目
在棱长为2的正方体ABCD-A1B1C1D1中，E，F分别为棱AB和CC1的中点，则线段EF被正方体的内切球球面截在球内的线段长为
 
．
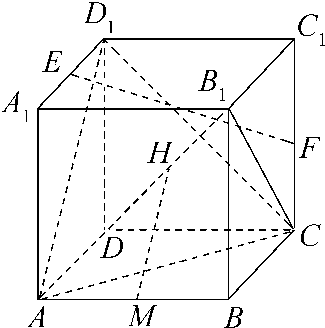精英家教网如图，在棱长为2的正方体ABCD-A1B1C1D1中，E、F、M、H分别为A1D1、CC1、AB、DB1的中点．
（1）求证：EF∥平面ACD1；
（2）求证：MH⊥B1C；
（3）在棱BB1上是否存在一点P，使得二面角P-AC-B的大小为30°？若存在，求出BP的长；若不存在，请说明理由．
在棱长为2的正方体ABCD-A1B1C1D1中，E、F分别为A1D1和CC1的中点
（1）求证：EF∥平面A1C1B；
（2）求异面直线EF与AB所成角的余弦值．
在棱长为2的正方体ABCD-A1B1C1D1中，点E，F分别是棱AB，BC的中点，则点C1到平面B1EF的距离是（　　）
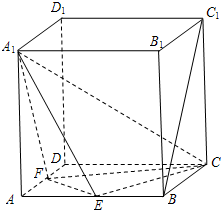（2007•静安区一模）（文）如图，在棱长为2的正方体ABCD-A1B1C1D1中，点E、F分别是棱AB、AD的中点．求：
（1）异面直线BC1与EF所成角的大小；
（2）三棱锥A1-EFC的体积V．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网