题目内容
12.在△ABC中,角A,B,C的对边分别为a,b,c,已知a2+c2-b2=ac,且$\sqrt{2}$b=$\sqrt{3}$c,求角A的大小.分析 由余弦定理求得cosB=$\frac{1}{2}$,求出角B的值,再由正弦定理可得sinC=$\frac{\sqrt{2}}{2}$求得C的值,即可求角A的大小.
解答 解:因为a2+c2-b2=ac,
所以b2=a2+c2-ac,
又因为b2=a2+c2-2accosB,所以cosB=$\frac{1}{2}$,
所以B=60°.
因为由$\sqrt{2}$b=$\sqrt{3}$c,所以$\sqrt{2}$sinB=$\sqrt{3}$sinC,
所以sinC=$\frac{\sqrt{2}}{2}$,所以C=45°,
所以A=75°.
点评 本题主要考查解三角形的方法,正弦定理、余弦定理的应用,根据三角函数的值求角,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
7.已知函数f(x)=ax+b是奇函数,且过点(4,-12),则a、b的值分别为( )
| A. | a=0,b=-3 | B. | a=-3,b=0 | C. | a=3,b=0 | D. | a=0,b=3 |
4.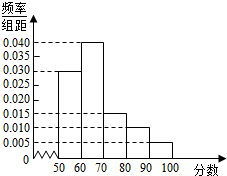 根据某组调查数据制作的频率分布直方图如图所示,则该组数据中的数位于区间(60,70)内的频率是( )
根据某组调查数据制作的频率分布直方图如图所示,则该组数据中的数位于区间(60,70)内的频率是( )
 根据某组调查数据制作的频率分布直方图如图所示,则该组数据中的数位于区间(60,70)内的频率是( )
根据某组调查数据制作的频率分布直方图如图所示,则该组数据中的数位于区间(60,70)内的频率是( )| A. | 0.004 | B. | 0.04 | C. | 0.4 | D. | 4 |