Question

如图，已知二面角α－PQ－β的大小为60°，点C为棱PQ上一点，A∈β，AC＝2，∠ACP＝30°，则点A到平面α的距离为(       )

 A．1　　　B． 　　　C．　　　D．

 

Answer 1

【答案】

C

【解析】本试题主要是考查了二面角的概念和点到面的距离的求解的运用。

过A作AO⊥α于O，点A到平面α的距离为AO；,作AD⊥PQ于D，连接OD，,则AD⊥CD，AO⊥OD，∠ADO就是二面角α-PQ-β的大小为60°．,∵AC=2，∠ACP=30°，所以AD=ACsin30°=2×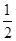=1．,在Rt△AOD中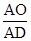，=sin60°，,AO=ADsin60°=1×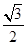=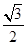,故选C.

解决该试题的关键是先作出二面角，然后根据得到点A到平面α的距离。