题目内容
下列命题:①若f(x)存在导函数,则f′(2x)=[f(2x)]′;
②若函数h(x)=cos4x-sin4x,则
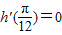 ;
;③若函数g(x)=(x-1)(x-2)(x-3)…(x-2012)(x-2013),则g′(2013)=2012!;
④函数
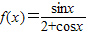 的单调递增区间是
的单调递增区间是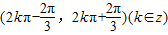
其中真命题为 .(填序号)
【答案】分析:分别利用导数的运算以及导数的应用进行判断即可.
解答:解:①[f(2x)]′=f′(2x)(2x)′=2f′(2x),所以①错误.
②因为h(x)=cos4x-sin4x=(cos2x+sin2x)(cos2x-sin2x)=cos2x,
所以h'(x)=-2sin2x,即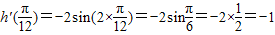 ,所以②错误.
,所以②错误.
③因为g(x)=(x-1)(x-2)(x-3)…(x-2012)(x-2013),
所以g'(x)=[(x-1)(x-2)…(x-2012)]+(x-2013)?[(x-1)(x-2)…(x-2012)]'
所以g'(2013)=(2013-1)(2013-2)…(2013-2012)=1×2×…×2012=2012!,所以③正确.
④函数的导数为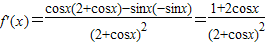 ,
,
由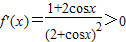 得1+2cosx>0,即
得1+2cosx>0,即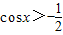 ,所以
,所以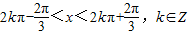 ,
,
即函数的单调递增区间为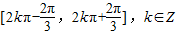 ,所以④正确.
,所以④正确.
故答案为:③④.
点评:本题主要考查导数的运算以及导数的应用,比较综合.
解答:解:①[f(2x)]′=f′(2x)(2x)′=2f′(2x),所以①错误.
②因为h(x)=cos4x-sin4x=(cos2x+sin2x)(cos2x-sin2x)=cos2x,
所以h'(x)=-2sin2x,即
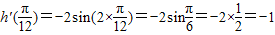 ,所以②错误.
,所以②错误.③因为g(x)=(x-1)(x-2)(x-3)…(x-2012)(x-2013),
所以g'(x)=[(x-1)(x-2)…(x-2012)]+(x-2013)?[(x-1)(x-2)…(x-2012)]'
所以g'(2013)=(2013-1)(2013-2)…(2013-2012)=1×2×…×2012=2012!,所以③正确.
④函数的导数为
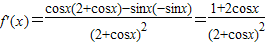 ,
,由
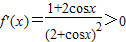 得1+2cosx>0,即
得1+2cosx>0,即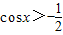 ,所以
,所以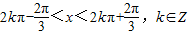 ,
,即函数的单调递增区间为
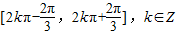 ,所以④正确.
,所以④正确.故答案为:③④.
点评:本题主要考查导数的运算以及导数的应用,比较综合.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
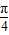 ,
,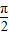 ),则f(sinθ)>f(cosθ);
),则f(sinθ)>f(cosθ);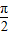 ;
;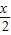 -1,则f(x+π)=f(x)对x∈R恒成立;
-1,则f(x+π)=f(x)对x∈R恒成立;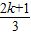 πx-
πx-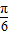 )(k∈N*)在区间[a,a+3]上的值
)(k∈N*)在区间[a,a+3]上的值 出现的次数不小于4次,又不多于8次,则k可以取2和3.
出现的次数不小于4次,又不多于8次,则k可以取2和3.