题目内容
直线AB与椭圆 相交于A、B两点,若点P(1,1)恰为弦AB的中点,则直线AB的方程为
相交于A、B两点,若点P(1,1)恰为弦AB的中点,则直线AB的方程为
- A.y=-2x-1
- B.
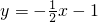
- C.y=-2x+3
- D.

C
分析:设A(x1,y1),B(x2,y2),则由中点坐标公式可求x1+x2,y1+y2,由A,B在椭圆上可得 ,
, ,两式相减可得,结合KAB=
,两式相减可得,结合KAB= ,代入可求直线AB的斜率,进而可求直线AB的方程
,代入可求直线AB的斜率,进而可求直线AB的方程
解答:设A(x1,y1),B(x2,y2),则 ,
,
由A,B在椭圆上可得 ,
,
两式相减可得,

∴KAB= =
= =-2
=-2
直线AB的方程为y-1=-2(x-1)即y=-2x+3
故选C
点评:本题主要考查了直线与椭圆相交关系的应用,要注意这种:设而不求”的解法在解题中的应用.
分析:设A(x1,y1),B(x2,y2),则由中点坐标公式可求x1+x2,y1+y2,由A,B在椭圆上可得
 ,
, ,两式相减可得,结合KAB=
,两式相减可得,结合KAB= ,代入可求直线AB的斜率,进而可求直线AB的方程
,代入可求直线AB的斜率,进而可求直线AB的方程解答:设A(x1,y1),B(x2,y2),则
 ,
,
由A,B在椭圆上可得
 ,
,
两式相减可得,


∴KAB=
 =
= =-2
=-2直线AB的方程为y-1=-2(x-1)即y=-2x+3
故选C
点评:本题主要考查了直线与椭圆相交关系的应用,要注意这种:设而不求”的解法在解题中的应用.

练习册系列答案
相关题目
 如图,点A(-a,0),B(
如图,点A(-a,0),B(