题目内容
在△ABC中,若cosAcosB>sinAsinB,则此三角形一定是
- A.钝角三角形
- B.直角三角形
- C.锐角三角形
- D.形状不确定
A
分析:先将条件等价于cos(A+B)>0,从而可知C为钝角,故可判断.
解答:由题意,∵cosAcosB>sinAsinB
∴cos(A+B)>0
∴cosC<0
∴C为钝角
故选A.
点评:本题以三角函数为载体,考查三角形的形状判断,关键是利用和角的余弦公式,求得C为钝角.
分析:先将条件等价于cos(A+B)>0,从而可知C为钝角,故可判断.
解答:由题意,∵cosAcosB>sinAsinB
∴cos(A+B)>0
∴cosC<0
∴C为钝角
故选A.
点评:本题以三角函数为载体,考查三角形的形状判断,关键是利用和角的余弦公式,求得C为钝角.

练习册系列答案
相关题目
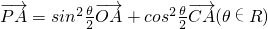 ,则
,则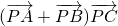 的最小值是________.
的最小值是________.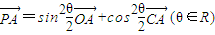 ,则
,则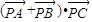 的最小值是 .
的最小值是 .