题目内容
已知f(x)=x2+px+q.
(1)求证:f(1)-2f(2)+f(3)=2;
(2)求证:|f(1)|、|f(2)|、|f(3)|中至少有一个不小于 .
.
(2)假设|f(1)|、|f(2)|、|f(3)|都小于 ,
,
则有|f(1)|< ,|f(2)|<
,|f(2)|< ,|f(3)|<
,|f(3)|< .
.
∴|f(1)|+2|f(2)|+|f(3)|<2.又|f(1)|+2|f(2)|+|f(3)|
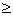 f(1)-2f(2)+f(3)=2,
f(1)-2f(2)+f(3)=2,
这与|f(1)|+2|f(2)|+|f(3)|<2矛盾.
∴假设不成立,从而原命题成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
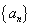 中,
中,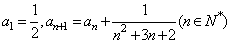 ,则数列
,则数列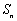 是等比数列
是等比数列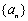 的前
的前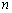 项和,
项和, ,
,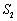 ,
, 成等差数列,且
成等差数列,且 .
.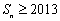 ?若存在,求出符合条件的所有
?若存在,求出符合条件的所有
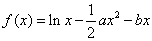
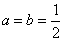 时,求函数
时,求函数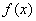 的单调区间;
的单调区间;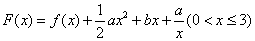 ,其图象上任意一点P(x0,y0)处切线的斜率k≤
,其图象上任意一点P(x0,y0)处切线的斜率k≤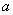 的取值范围;
的取值范围;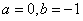 时,方程
时,方程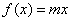 在区间内有唯一实数解,求实数
在区间内有唯一实数解,求实数 的取值范围.
的取值范围.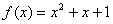 在点(0,1)处的切线方程为( )
在点(0,1)处的切线方程为( )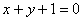 B.
B.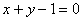
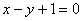 D.
D.
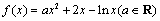 .
.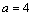 ,求函数
,求函数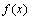 的极值;
的极值;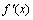 在
在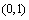 有唯一的零点
有唯一的零点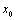 ,求
,求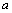 的取值范围;
的取值范围;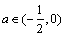 ,设
,设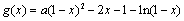 ,求证:
,求证: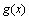 在
在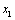 ,且对(Ⅱ)中的
,且对(Ⅱ)中的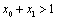 .
.