题目内容
已知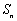 是等比数列
是等比数列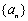 的前
的前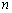 项和,
项和, ,
,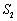 ,
, 成等差数列,且
成等差数列,且 .
.
(Ⅰ)求数列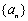 的通项公式;
的通项公式;
(Ⅱ)是否存在正整数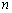 ,使得
,使得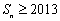 ?若存在,求出符合条件的所有
?若存在,求出符合条件的所有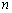 的集合;若不存在,说明理由.
的集合;若不存在,说明理由.
【答案】(Ⅰ)设数列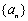 的公比为
的公比为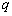 ,则
,则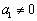 ,
,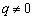 . 由题意得
. 由题意得
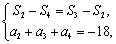 即
即 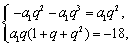
解得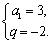
故数列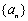 的通项公式为
的通项公式为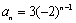 .
.
(Ⅱ)由(Ⅰ)有 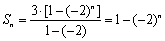 .
.
若存在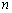 ,使得
,使得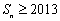 ,则
,则 ,即
,即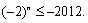
当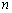 为偶数时,
为偶数时,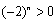 , 上式不成立;
, 上式不成立;
当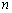 为奇数时,
为奇数时, ,即
,即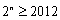 ,则
,则 .
.
综上,存在符合条件的正整数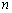 ,且所有这样的n的集合为
,且所有这样的n的集合为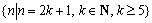 .
.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
 的不等式
的不等式 (
( )的解集为
)的解集为 ,且
,且 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
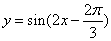 的图像, 需要将函数
的图像, 需要将函数 的图像( )
的图像( ) 个单位 B.向右平移
个单位 B.向右平移 个单位 D.向左平移
个单位 D.向左平移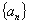 的前
的前 项和为
项和为 ,已知
,已知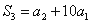 ,
,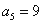 ,则
,则
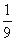 (B)
(B)  (C)
(C) 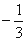 (D)
(D)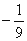
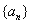 的公差
的公差 ,前
,前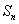 .
.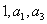 成等比数列,求
成等比数列,求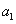 ;
; ,求
,求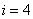 ,那么空白的判断框中应填人的条件是 ( )
,那么空白的判断框中应填人的条件是 ( )
 .
. P到直线y=x-2的距离的最小值是 ( )
P到直线y=x-2的距离的最小值是 ( ) C. 2 D.
C. 2 D. 