题目内容
已知集合D={(x1,x2)|x1>0,x2>0,x1+x2=k}(其中k为正常数).(1)设u=x1x2,求u的取值范围;
(2)求证:当k≥1时不等式
 对任意(x1,x2)∈D恒成立;
对任意(x1,x2)∈D恒成立;(3)求使不等式
 对任意(x1,x2)∈D恒成立的k2的范围.
对任意(x1,x2)∈D恒成立的k2的范围.
【答案】分析:(1)利用基本不等式,其中和为定值,积有最大值;
(2)结合(1)中的范围直接将左边展开,利用u在 上单调递增即可,或者作差法比较;
上单调递增即可,或者作差法比较;
(3)结合(2)将(3)转化为求使 对
对 恒成立的k的范围,利用函数的单调性解决,或者作差法求解.
恒成立的k的范围,利用函数的单调性解决,或者作差法求解.
解答:解:(1) ,当且仅当
,当且仅当 时等号成立,
时等号成立,
故u的取值范围为 .
.
(2)解法一(函数法) =
=
由 ,又k≥1,k2-1≥0,
,又k≥1,k2-1≥0,
∴在 上是增函数
上是增函数
所以
=

即当k≥1时不等式 成立.
成立.
解法二(不等式证明的作差比较法)

=
=
= ,
,
将k2-4x1x2=(x1-x2)2代入得:

=
∵(x1-x2)2≥0,k≥1时4-k2x1x2-4k2=4(1-k2)-k2x1x2<0,
∴ ,
,
即当k≥1时不等式 成立.
成立.
(3)解法一(函数法)
记 =
= ,
,
则 ,
,
即求使 对
对 恒成立的k2的范围.
恒成立的k2的范围.
由(2)知,要使
对任意(x1,x2)∈D恒成立,必有0<k<1,
因此1-k2>0,
∴函数 在
在 上递减,在
上递减,在 上递增,
上递增,
要使函数f(u)在 上恒有
上恒有 ,必有
,必有 ,即k4+16k2-16≤0,
,即k4+16k2-16≤0,
解得 .
.
解法二(不等式证明的作差比较法)
由(2)可知 =
= ,
,
要不等式恒成立,必须4-k2x1x2-4k2≥0恒成立
即 恒成立
恒成立
由 得
得 ,即k4+16k2-16≤0,
,即k4+16k2-16≤0,
解得 .
.
因此不等式 恒成立的k2的范围是
恒成立的k2的范围是
点评:本题考查不等式的综合应用,以及利用转化思想、函数思想转化为函数问题利用函数的单调性解决不等式问题,属于中档题.
(2)结合(1)中的范围直接将左边展开,利用u在
 上单调递增即可,或者作差法比较;
上单调递增即可,或者作差法比较;(3)结合(2)将(3)转化为求使
 对
对 恒成立的k的范围,利用函数的单调性解决,或者作差法求解.
恒成立的k的范围,利用函数的单调性解决,或者作差法求解.解答:解:(1)
 ,当且仅当
,当且仅当 时等号成立,
时等号成立,故u的取值范围为
 .
.(2)解法一(函数法)
 =
=
由
 ,又k≥1,k2-1≥0,
,又k≥1,k2-1≥0,∴在
 上是增函数
上是增函数所以

=


即当k≥1时不等式
 成立.
成立.解法二(不等式证明的作差比较法)

=

=

=
 ,
,将k2-4x1x2=(x1-x2)2代入得:

=

∵(x1-x2)2≥0,k≥1时4-k2x1x2-4k2=4(1-k2)-k2x1x2<0,
∴
 ,
,即当k≥1时不等式
 成立.
成立.(3)解法一(函数法)
记
 =
= ,
,则
 ,
,即求使
 对
对 恒成立的k2的范围.
恒成立的k2的范围.由(2)知,要使

对任意(x1,x2)∈D恒成立,必有0<k<1,
因此1-k2>0,
∴函数
 在
在 上递减,在
上递减,在 上递增,
上递增,要使函数f(u)在
 上恒有
上恒有 ,必有
,必有 ,即k4+16k2-16≤0,
,即k4+16k2-16≤0,解得
 .
.解法二(不等式证明的作差比较法)
由(2)可知
 =
= ,
,要不等式恒成立,必须4-k2x1x2-4k2≥0恒成立
即
 恒成立
恒成立由
 得
得 ,即k4+16k2-16≤0,
,即k4+16k2-16≤0,解得
 .
.因此不等式
 恒成立的k2的范围是
恒成立的k2的范围是
点评:本题考查不等式的综合应用,以及利用转化思想、函数思想转化为函数问题利用函数的单调性解决不等式问题,属于中档题.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目

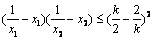 对任意(x1,x2) ∈D恒成立;
对任意(x1,x2) ∈D恒成立;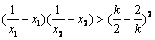 对任意(x1,x2) ∈D恒成立的k的范围.
对任意(x1,x2) ∈D恒成立的k的范围.