题目内容
已知圆C上一点A(2,3),直线2x+y=0平分圆C,且圆C与直线x-y+1=0相交的弦长为2
,求圆C的方程.
| 2 |
设圆的方程为:(x-a)2+(y-b)2=r2
∵直线2x+y=0平分圆,
则:圆心在直线2x+y=0上,则2a+b=0?b=-2a(2分)
又直线x-y+1=0与圆相交所得的弦长为2
,
由圆的几何性质可得:圆心到该直线的距离为
(2分)
即:
=
?
=
?r2=
+2(2分)
∴该圆的方程为(x-a)2+(y+2a)2=
+2,
把A的坐标(2,3)代入圆的方程得:a2+10a+21=0,
解得:a=-3或a=-7,
∴圆的方程为:(x+3)2+(y-6)2=34或(x+7)2+(y-14)2=202.
∵直线2x+y=0平分圆,
则:圆心在直线2x+y=0上,则2a+b=0?b=-2a(2分)
又直线x-y+1=0与圆相交所得的弦长为2
| 2 |
由圆的几何性质可得:圆心到该直线的距离为
| r2-2 |
即:
| |a-b+1| | ||
|
| r2-2 |
| |3a+1| | ||
|
| r2-2 |
| (3a+1)2 |
| 2 |
∴该圆的方程为(x-a)2+(y+2a)2=
| (3a+1)2 |
| 2 |
把A的坐标(2,3)代入圆的方程得:a2+10a+21=0,
解得:a=-3或a=-7,
∴圆的方程为:(x+3)2+(y-6)2=34或(x+7)2+(y-14)2=202.

练习册系列答案
相关题目
 ,求圆C的方程.
,求圆C的方程.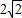 ,求圆C的方程.
,求圆C的方程.