题目内容
(本小题满分18分)在直角坐标系![]() 中,点P到两点
中,点P到两点![]() ,
,![]() 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为![]() ,直线
,直线![]() 与C交于A,B两点.
与C交于A,B两点.
(Ⅰ)写出C的方程;
(Ⅱ)若![]()
![]()
![]() ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有|![]() |>|
|>|![]() |.
|.
解:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以![]() 为焦点,长半轴为2的椭圆.它的短半轴
为焦点,长半轴为2的椭圆.它的短半轴![]() ,
,
故曲线C的方程为![]() .
.
(Ⅱ)设![]() ,其坐标满足
,其坐标满足
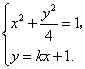 消去y并整理得
消去y并整理得![]() ,
,
故![]() .
.
若![]() ,即
,即![]() . 而
. 而![]() ,
,
于是![]() ,
,
化简得![]() ,所以
,所以![]() .
.
(Ⅲ)![]()
![]()
![]()
![]() .
.
因为A在第一象限,故![]() .由
.由![]() 知
知![]() ,从而
,从而![]() .又
.又![]() ,
,
故![]() ,
,
即在题设条件下,恒有![]() .
.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 (本小题满分18分)如图,将圆分成
(本小题满分18分)如图,将圆分成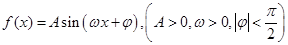 的图象的一部分如下图所示。
的图象的一部分如下图所示。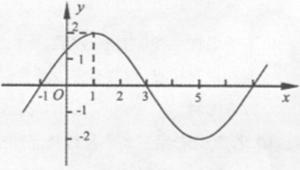
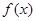 的解析式;
的解析式;
 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围;