题目内容
19．设f（x）是定义在R+上的函数，且满足条件：（1）f（xy）=f（x）+f（y）；（2）f（2）=1；（3）在（0，+∞）上是增函数，如果f（x）+f（x-3）≤2，求x的取值范围．分析 利用函数关系结合函数的单调性将不等式进行转化进行求解即可．
解答 解：∵f（2）=1，
∴f（4）=f（2）+f（2）=1+1=2，
则不等式f（x）+f（x-3）≤2等价为f（x（x-3））≤f（4），
∵在（0，+∞）上是增函数，
∴$\left\{\begin{array}{l}{x＞0}\\{x-3＞0}\\{x（x-3）≤4}\end{array}\right.$，即$\left\{\begin{array}{l}{x＞0}\\{x＞3}\\{{x}^{2}-3x-4≤0}\end{array}\right.$，即$\left\{\begin{array}{l}{x＞0}\\{x＞3}\\{-1≤x≤4}\end{array}\right.$，
解得3＜x≤4，
即不等式的解集为（3，4]．
点评 本题主要考查抽象函数的应用，根据函数单调性的性质是解决本题的关键．
练习册系列答案
相关题目
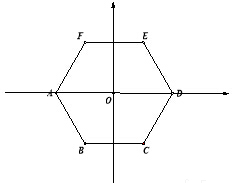已知正六边形ABCDEF的边长是2，以正六边形中心为原点，以对角线AD所在的直线为x轴，如图建立平面直角坐标系．
9．命题“?x∈R，x2+1≥0”的否定是 （ ）
| A． | $?{x_0}∈R，{x_0}^2+1≥0$ | B． | $?{x_0}∈R，{x_0}^2+1＜0$ | ||
| C． | $?{x_0}∈R，{x_0}^2+1≤0$ | D． | ?x∈R，x2+1＜0 |