题目内容
(2009•枣庄一模)已知函数f(x)=sin
x,a等于抛掷一颗骰子得到的点数,则y=f(x)在[0,4]上至少有5个零点的概率是( )
| aπ |
| 3 |
分析:y=f(x)在[0,4]上至少有5个零点,等价于函数f(x)的周期小于或等于2,即
≤2,可得a=3、4、5、6,共计4个值.而所有的a值共计6个,由此求得y=f(x)在[0,4]上至少有5个零点的概率.
| 2π | ||
|
解答:解:y=f(x)在[0,4]上至少有5个零点,等价于函数f(x)的周期小于或等于2,
即
≤2,解得a≥3,故a=3、4、5、6.
而所有的a值共计6个,故y=f(x)在[0,4]上至少有5个零点的概率是
=
,
故选C.
即
| 2π | ||
|
而所有的a值共计6个,故y=f(x)在[0,4]上至少有5个零点的概率是
| 4 |
| 6 |
| 2 |
| 3 |
故选C.
点评:本题主要考查函数的零点的定义,古典概率及其计算公式的应用,属于基础题.

练习册系列答案
相关题目
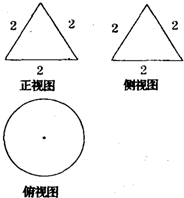 (2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )
(2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )