题目内容
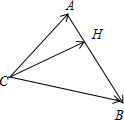如图，在△ABC中，已知CA=2，CB=3，∠ACB=60°，CH为AB边上的高．（1）求
| AB |
| BC |
（2）设
| CH |
| CB |
| CA |
分析：（1）利用向量的运算法则和数量积即可得出；
（2）利用向量共线、垂直与数量积的关系即可得出．
（2）利用向量共线、垂直与数量积的关系即可得出．
解答：解：（1）∵
=
+
，
∴
•
=（
+
）•
=
•
-
2=2×3cos60°-32=3-9=-6；
（2）∵三点A、H、B共线，∴存在实数λ使得
=λ
．
又∵
=
+
，
=
-
，
∴
=(1-λ)
+λ
．好
∵CH⊥AB，
∴
•
=(m
+n
)•
=0，
∴(m
+n
)•(
-
)=0，
化为m
2-m
•
+n
•
-n
2=0，
化为n=6m．
比较
=(1-λ)
+λ
，
=m
+n
，得m+n=1．
联立
，解得
．
∴m=
，n=
．
| AB |
| AC |
| CB |
∴
| AB |
| BC |
| AC |
| CB |
| BC |
| AC |
| BC |
| BC |
（2）∵三点A、H、B共线，∴存在实数λ使得
| AH |
| AB |
又∵
| CH |
| CA |
| AH |
| AB |
| CB |
| CA |
∴
| CH |
| CA |
| CB |
∵CH⊥AB，
∴
| CH |
| AB |
| CB |
| CA |
| AB |
∴(m
| CB |
| CA |
| CB |
| CA |
化为m
| CB |
| CB |
| CA |
| CA |
| CB |
| CA |
化为n=6m．
比较
| CH |
| CA |
| CB |
| CH |
| CB |
| CA |
联立
|
|
∴m=
| 1 |
| 7 |
| 6 |
| 7 |
点评：熟练掌握向量的运算法则、数量积的计算公式、向量共线定理、垂直与数量积的关系是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，在△ABC中，已知∠ABC=90°，AB上一点E，以BE为直径的⊙O恰与AC相切于点D，若AE=2cm，
如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在△ABC中，设
如图，在△ABC中，∠B=45°，D是BC边上的一点，AD=5，AC=7，DC=3．
如图，在△ABC中，已知