题目内容
（本小题满分12分）
已知四棱锥P—ABCD中，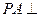
平面ABCD，底面ABCD为菱形，
，AB=PA=2，E、F分别为BC、PD的中点。
（1）求证：PB//平面AFC；
（2）求平面PAE与平面PCD所成锐二面角的余弦值。
已知四棱锥P—ABCD中，
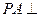平面ABCD，底面ABCD为菱形，，AB=PA=2，E、F分别为BC、PD的中点。（1）求证：PB//平面AFC；
（2）求平面PAE与平面PCD所成锐二面角的余弦值。
（1）略
（2）平面PAE与平面PCD所成锐二面角的余弦值为
（2）平面PAE与平面PCD所成锐二面角的余弦值为
解：（1）连结BD交AC于O，
为菱形，则BO=OD…………1分
连结FO，
…………3分
平面AFC，
平面AFC，
平面AFC…………4分
（2）
为BC中点，
…………6分
建立如图所示的空间直角坐标系，
，
则
，D（90，2，0）…………8分
平面PAE的一个法向量为
……9分
设平面PDC的一个法向量为
则
…………11分
平面PAE与平面PCD所成锐二面角的余弦值为……12分
为菱形，则BO=OD…………1分连结FO，
…………3分平面AFC，平面AFC，平面AFC…………4分（2）
为BC中点，…………6分建立如图所示的空间直角坐标系，
，则
，D（90，2，0）…………8分平面PAE的一个法向量为
……9分设平面PDC的一个法向量为
则
…………11分平面PAE与平面PCD所成锐二面角的余弦值为……12分
练习册系列答案
相关题目
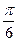.∠AOQ＝α，α∈[0，π）.（Ⅰ）若Q（
，
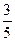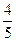），求cos（α－
·
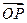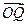，求f（α）的值域．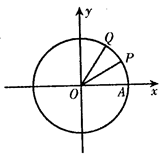
中，E、F分别为棱BC和
—l—
为60
，点A
，点A到平面
，那么点A在
到平面
所成的角是 、直线
和平面
所成的角为 .
，当
中，
于
，三边分别是
，则有
；类比上述结论，写出下列条件下的结论：四面体
中，
的面积分别是
，二面角
的度数分别是
，则
．