题目内容
17. 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,BC∥AD且2BC=AD,∠PBC=90°,∠PBA≠90°.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,BC∥AD且2BC=AD,∠PBC=90°,∠PBA≠90°.(1)求证:平面PBC⊥平面PAB;
(2)若平面PAB∩平面PCD=l,求证:直线l不平行于平面ABCD.(用反证法证明)
分析 (1)自P作PH⊥AB于H,由平面PAB⊥平面ABCD,可得PH⊥平面ABCD.于是BC⊥PH.又BC⊥PB,可得BC⊥平面PAB,即可证明平面PBC⊥平面PAB;
(2)利用反证法,证明AB∥CD,即四边形ABCD为平行四边形,得到矛盾即可得到结论.
解答  (1)证明:自P作PH⊥AB于H,
(1)证明:自P作PH⊥AB于H,
因为平面PAB⊥平面ABCD,且平面PAB∩平面ABCD=AB,PH?平面PAB,
所以PH⊥平面ABCD.
因为BC?平面ABCD,
所以BC⊥PH.
因为∠PBC=90°,
所以BC⊥PB,
而∠PBA≠90°,于是点H与B不重合,即PB∩PH=P.
因为PB,PH?平面PAB,
所以BC⊥平面PAB.
因为BC?平面PBC,
故平面PBC⊥平面PAB;
(2)不平行,
反证法:
假设直线l平行于平面ABCD,
由于l?平面PCD,且平面PCD∩平面ABCD=CD,
∴l∥CD,
同理可得l∥AB,
即AB∥CD,
∵BC∥AD,
∴四边形ABCD为梯形,
则AD=BC,与2BC=AD矛盾,
故假设不成立,
即直线l不平行于平面ABCD.
点评 本题主要考查面面垂直和线面平行的判定,要求熟练掌握相应的判定定理.

练习册系列答案
相关题目
6.已知a∈R,函数f(x)=-$\frac{3}{2}$x2+(4a+2)x-a(a+2)lnx在(0,1)内有极值,则a的取值范围是( )
| A. | (0,1) | B. | (-2,0)∪(0,1) | C. | (-2,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1) | D. | (-2,1) |
 在如图所示的正方体ABCD-A1B1C1D1的12条棱所在直线中,与直线AB异面的直线有4条.
在如图所示的正方体ABCD-A1B1C1D1的12条棱所在直线中,与直线AB异面的直线有4条.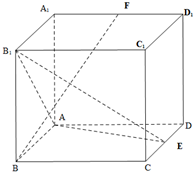 如图:在长方体ABCD-A1B1C1D1中,AB=2,BC=4,BB1=4,E是CD的中点,F是A1D1的中点.
如图:在长方体ABCD-A1B1C1D1中,AB=2,BC=4,BB1=4,E是CD的中点,F是A1D1的中点. AC=BC=$\sqrt{2}$,CD=DE=1,AB=BE=EA=2,CD⊥面ABC.
AC=BC=$\sqrt{2}$,CD=DE=1,AB=BE=EA=2,CD⊥面ABC. 已知AB是⊙O的直径,直线AF交⊙O于F(不与B重合),直线EC与⊙O相切于C,交AB于E,连接AC,且∠OAC=∠CAF,求证:
已知AB是⊙O的直径,直线AF交⊙O于F(不与B重合),直线EC与⊙O相切于C,交AB于E,连接AC,且∠OAC=∠CAF,求证: