题目内容
（
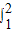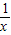+x）dx=（ ）A．ln2+
B．ln2+
C．ln2-
D．ln2+3
【答案】分析：由定积分运算公式，求出函数的f（x）=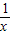
+x的一个原函数F（x）=lnx+
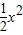，利用微积分基本定理即可得到所求积分的值．
解答：解：由积分运算法则，得
（
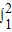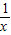+x）dx=（lnx+
）
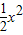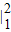
=（ln2+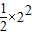
）-（ln1+
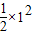）=ln2+
故选：A
点评：本题求一个定积分的值，着重考查了定积分计算公式和微积分基本定理等知识，属于基础题．
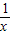+x的一个原函数F（x）=lnx+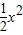，利用微积分基本定理即可得到所求积分的值．解答：解：由积分运算法则，得
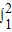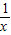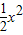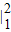
（+x）dx=（lnx+）=（ln2+
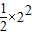）-（ln1+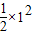）=ln2+故选：A
点评：本题求一个定积分的值，着重考查了定积分计算公式和微积分基本定理等知识，属于基础题．
练习册系列答案
相关题目
设函数f（x）=xm+ax的导函数f′（x）=2x+1，则
f（-x）dx的值等于（ ）
| ∫ | 2 1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数y=f（x）的定义域为R+，若对于给定的正数K，定义函数fK(x)=
，则当函数f（x）=
，K=1时，
fK（x）dx的值为（ ）
|
| 1 |
| x |
| ∫ | 2
|
| A、2ln2 |
| B、2ln2-1 |
| C、2ln2 |
| D、2ln2+1 |