题目内容
已知函数 (其中a,b为常数)的图象经过(1,2),
(其中a,b为常数)的图象经过(1,2),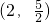 两点.
两点.
(1)求函数f(x)的解析式;
(2)证明函数在[1,+∞)上是增函数;
(3)若不等式 对任意的
对任意的 恒成立,求实数a的取值集合.
恒成立,求实数a的取值集合.
解:(1)∵函数 (其中a,b为常数)的图象经过(1,2),
(其中a,b为常数)的图象经过(1,2),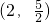 两点,
两点,
∴ ,解得a=1,b=1,
,解得a=1,b=1,
∴ .…..
.…..
(2)设x2>x1≥1,则
= ,
,
∵x2>x1≥1,∴x1x2>0,x2-x1>0,x1x2>1,
∴x1x2-1>0,
故f(x2)-f(x1)>0,即f(x2)>f(x1),
所以f(x)在[1,+∞)上是增函数. …
(3)要使不等式 对任意的
对任意的 恒成立,
恒成立,
只需 ,
, ,
,
由(2)知f(x)在[1,+∞)上单调递增,
同理可证f(x)在(0,1]上单调递减.
当 时,f(x)在
时,f(x)在 上单调递减,f(x)在[1,3]上单调递增.
上单调递减,f(x)在[1,3]上单调递增.
又 ,
, ,
,
∴当 时,
时, ,
,
∴ ,
,
∴a的取值集合是{a|a≥log25}.…
分析:(1)由函数 (其中a,b为常数)的图象经过(1,2),
(其中a,b为常数)的图象经过(1,2),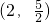 两点,列方程能求出函数f(x)的解析式.
两点,列方程能求出函数f(x)的解析式.
(2)设x2>x1≥1,推导出f(x1)-f(x2)= ,由此能够证明f(x)在[1,+∞)上是增函数.
,由此能够证明f(x)在[1,+∞)上是增函数.
(3)要使不等式 对任意的
对任意的 恒成立,只需
恒成立,只需 ,
, ,由此能求出a的取值集合.
,由此能求出a的取值集合.
点评:本题考查函数解析式的求法,考查函数单调性的证明,考查实数的取值集合的求法,解题时要认真审题,仔细解答,注意定义法和等价转化思想的合理运用.
 (其中a,b为常数)的图象经过(1,2),
(其中a,b为常数)的图象经过(1,2),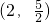 两点,
两点,∴
 ,解得a=1,b=1,
,解得a=1,b=1,∴
 .…..
.…..(2)设x2>x1≥1,则

=
 ,
,∵x2>x1≥1,∴x1x2>0,x2-x1>0,x1x2>1,
∴x1x2-1>0,
故f(x2)-f(x1)>0,即f(x2)>f(x1),
所以f(x)在[1,+∞)上是增函数. …
(3)要使不等式
 对任意的
对任意的 恒成立,
恒成立,只需
 ,
, ,
,由(2)知f(x)在[1,+∞)上单调递增,
同理可证f(x)在(0,1]上单调递减.
当
 时,f(x)在
时,f(x)在 上单调递减,f(x)在[1,3]上单调递增.
上单调递减,f(x)在[1,3]上单调递增.又
 ,
, ,
,∴当
 时,
时, ,
,∴
 ,
,∴a的取值集合是{a|a≥log25}.…
分析:(1)由函数
 (其中a,b为常数)的图象经过(1,2),
(其中a,b为常数)的图象经过(1,2),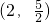 两点,列方程能求出函数f(x)的解析式.
两点,列方程能求出函数f(x)的解析式.(2)设x2>x1≥1,推导出f(x1)-f(x2)=
 ,由此能够证明f(x)在[1,+∞)上是增函数.
,由此能够证明f(x)在[1,+∞)上是增函数.(3)要使不等式
 对任意的
对任意的 恒成立,只需
恒成立,只需 ,
, ,由此能求出a的取值集合.
,由此能求出a的取值集合.点评:本题考查函数解析式的求法,考查函数单调性的证明,考查实数的取值集合的求法,解题时要认真审题,仔细解答,注意定义法和等价转化思想的合理运用.

练习册系列答案
相关题目
 ,其中a,b∈R.
,其中a,b∈R. ,不等式f(x)≤10在
,不等式f(x)≤10在 上恒成立,求b的取值范围.
上恒成立,求b的取值范围. ,其中a,b为常数.
,其中a,b为常数. ,其中a,b∈R.
,其中a,b∈R. ,不等式f(x)≤10在
,不等式f(x)≤10在 上恒成立,求b的取值范围.
上恒成立,求b的取值范围. (其中a,b为常数且
(其中a,b为常数且 )的反函数的图象经过点A(4,1)和B(16,3)。
)的反函数的图象经过点A(4,1)和B(16,3)。 在
在 上恒成立,求实数m的取值范围。
上恒成立,求实数m的取值范围。