题目内容
复数z满足|z+3-
思路分析:动点Z到定点(-3, ![]() )的距离为定长
)的距离为定长![]() ,轨迹为圆,据此可解之.
,轨迹为圆,据此可解之.
?
解法一:|z+3-![]() i|=
i|=![]() 对应的复数z在复平面内所表示的图形为以-3+
对应的复数z在复平面内所表示的图形为以-3+![]() i对应的点P为圆心,以
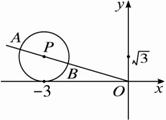
i对应的点P为圆心,以![]() 为半径的圆,|z|则表示圆上的点Z到原点的距离,如图所示,OP的连线交此圆于A、B两点,显然|OA|为最大距离,|OB|为最小距离,即?
为半径的圆,|z|则表示圆上的点Z到原点的距离,如图所示,OP的连线交此圆于A、B两点,显然|OA|为最大距离,|OB|为最小距离,即?
|z|最大=|OP|+![]() =
=![]() +
+![]() =3
=3![]() ,?
,?
|z|最小=|OP|-![]() =2
=2![]() -
-![]() =
=![]() .?
.?
解法二:∵||z|-|3-![]() i||≤|z+3-
i||≤|z+3-![]() i|≤|z|+|3-
i|≤|z|+|3-![]() i|,?
i|,?
又∵|z+3-![]() i|=
i|=![]() ,|3-
,|3-![]() i|=2
i|=2![]() ,?
,?
∴||z|-2![]() |≤
|≤![]() ,?
,?
即![]() ≤|z|≤3
≤|z|≤3![]() .?
.?
因此,|z|的最大值为3![]() ,最小值为
,最小值为![]() .
.
温馨提示:解法一充分利用复数模的几何意义,通过数形结合,充分利用形的直观、形象的特点,简化了对问题的处理方法;解法二则利用复数模的不等式:||z1|-|z2||≤|z1+z2|≤|z1|+|z2|,通过构造关于|z|的不等式,达到解题目的.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
若复数z满足|z+4+3i|=3,则复数z的模应满足的不等式是( )
| A、5≤|z|≤8 | B、2≤|z|≤8 | C、|z|≤5 | D、|z|<8 |
复数z满足|z-3|=|z+3|,且|z|=5,则z等于( )
| A、±5 | B、±5i | C、±3+5i | D、±3±4i |
已知复数z满足z=
(i为虚数单位),则复数
所对应的点所在象限为( )
| (3+i)2 |
| 1+i |
. |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |