题目内容
已知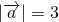 ,|
,| |=2,
|=2, 与
与 的夹角为60°,如果(3
的夹角为60°,如果(3 +5
+5 )⊥(m
)⊥(m -
- ),则m的值为
),则m的值为
- A.

- B.

- C.

- D.

C
分析:由(3 +5
+5 )⊥(m
)⊥(m -
- ),我们易得到(3
),我们易得到(3 +5
+5 )•(m
)•(m -
- )=0,结合
)=0,结合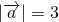 ,|
,| |=2,
|=2, 与
与 的夹角为60°,我们易得到一个关于m的方程,解方程即可得到答案.
的夹角为60°,我们易得到一个关于m的方程,解方程即可得到答案.
解答:∵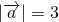 ,|
,| |=2,
|=2, 与
与 的夹角为60°
的夹角为60°
∴ =9,|
=9,| |2=4,
|2=4, •
• =3
=3
则(3 +5
+5 )•(m
)•(m -
- )
)
=3m -5|
-5| |2+(5m-3)
|2+(5m-3) •
•
=27m-20+3(5m-3)
=42m-29
又∵(3 +5
+5 )⊥(m
)⊥(m -
- ),
),
∴42m-29=0
∴m=
故选C
点评:本题考查的知识点是平面向量数量积坐标表示的应用,其中根据(3 +5
+5 )⊥(m
)⊥(m -
- ),得到(3
),得到(3 +5
+5 )•(m
)•(m -
- )=0,进而得到关于m的方程,是解答本类问题的关键.
)=0,进而得到关于m的方程,是解答本类问题的关键.
分析:由(3
 +5
+5 )⊥(m
)⊥(m -
- ),我们易得到(3
),我们易得到(3 +5
+5 )•(m
)•(m -
- )=0,结合
)=0,结合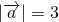 ,|
,| |=2,
|=2, 与
与 的夹角为60°,我们易得到一个关于m的方程,解方程即可得到答案.
的夹角为60°,我们易得到一个关于m的方程,解方程即可得到答案.解答:∵
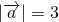 ,|
,| |=2,
|=2, 与
与 的夹角为60°
的夹角为60°∴
 =9,|
=9,| |2=4,
|2=4, •
• =3
=3则(3
 +5
+5 )•(m
)•(m -
- )
)=3m
 -5|
-5| |2+(5m-3)
|2+(5m-3) •
•
=27m-20+3(5m-3)
=42m-29
又∵(3
 +5
+5 )⊥(m
)⊥(m -
- ),
),∴42m-29=0
∴m=

故选C
点评:本题考查的知识点是平面向量数量积坐标表示的应用,其中根据(3
 +5
+5 )⊥(m
)⊥(m -
- ),得到(3
),得到(3 +5
+5 )•(m
)•(m -
- )=0,进而得到关于m的方程,是解答本类问题的关键.
)=0,进而得到关于m的方程,是解答本类问题的关键. 
练习册系列答案
相关题目
 =(1,0),
=(1,0), =(1,1),
=(1,1), =(-1,0),求λ和μ,使
=(-1,0),求λ和μ,使 ,|
,| ,|
,| |=2,
|=2, 与
与 的夹角为60°,如果(3
的夹角为60°,如果(3 +5
+5 )⊥(m
)⊥(m -
- ),则m的值为( )
),则m的值为( )



 ,|
,| |=2,
|=2, 与
与 的夹角为60°,如果(3
的夹角为60°,如果(3 +5
+5 )⊥(m
)⊥(m -
- ),则m的值为( )
),则m的值为( )



 =(1,0),
=(1,0), =(1,1),
=(1,1), =(-1,0),求λ和μ,使
=(-1,0),求λ和μ,使 ,|
,|