题目内容
设函数 .
.
(1)若 在
在 和
和 处有不同的极值,且极大值为4,
处有不同的极值,且极大值为4,
极小值为1,求 及实数
及实数 的值;
的值;
(2) 若 在
在 上单调递增且
上单调递增且 ,求
,求 的最大值.
的最大值.
【答案】
 ,
,
【解析】解:(1) ,依题意得:
,依题意得:

又 ,则
,则 ,
,
所以当 时,
时, ;当
;当 或
或 时,
时, ,
,
故 时函数有极大值,
时函数有极大值, 时函数有极小值;
时函数有极小值;
则 得
得
(2)  ,因为
,因为 在
在 上单调递增,且
上单调递增,且 ,所以
,所以 在
在 上恒成立。
上恒成立。
即 在
在 上恒成立,所以
上恒成立,所以 ,即
,即 的最大值为
的最大值为

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
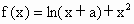 .
.
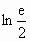 .
.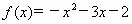 ;
;
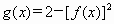 ,求
,求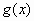 的解析式;
的解析式;
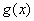 的图象;
的图象;
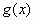 的零点(精确度0.1).
的零点(精确度0.1). .
. ,求
,求 的取值范围;
的取值范围; 的最值,并给出取最值时对应的
的最值,并给出取最值时对应的 的值
的值